��Ŀ����
����Ŀ����֪f(x)Ϊ������R�ϵ�ż��������x��0ʱ����f(x��1)����f(x)���ҵ�x��[0,1)ʱ��f(x)��log2(x��1)��������������
��f(2014)��f(��2015)��0��
������f(x)�ڶ�������������Ϊ2�ĺ�����
��ֱ��y��x�뺯��f(x)��ͼ����2�����㣻
������f(x)��ֵ��Ϊ(��1,1)��
������ȷ����(����)
A. �٢� B. �ڢ�
C. �٢� D. �٢ڢۢ�
���𰸡�C
�����������ڵ�x��0ʱ����f(x��1)����f(x)������f(x��2)����f(x��1)��f(x)��
�Ӷ���x��[1,2)ʱ��x��1��[0,1)����f(x��1)��log2x��
��f((x��1)��1)����f(x��1)f(x��1)����f(x)��log2xf(x)����log2x
��f(x)��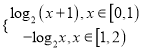 ��
��
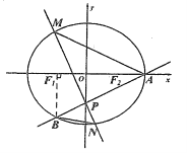
��ע��f(x)Ϊ������R�ϵ�ż���������Կ���������f(x)��ͼ�����£�
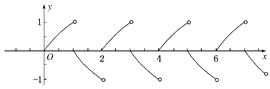
���ڢ�f(2014)��f(��2015)��f(2��1007��0)��f(2015)
��f(0)��f(2��1007��1)��0��f(1)����log21��0���ʢ���ȷ���ų�B��
���ڢ���ͼ���֪�����������ں������ʢ��Ǵ���ģ��ų�A��D��
���ڢ���ͼ���ֱ֪��y��x�뺯��f(x)��ͼ��ֻ��1�����㣬�ʢ۴���
���ڢ���ͼ���֪������ֵ��Ϊ(��1,1)���ʢ���ȷ��
��ѡC.
�㾦: ��������ż�������������ϵ���������ֵ���⣬��������ż�Լ������Խ��б任����������ֵ���Ա���ת������֪����ʽ�ĺ�������������⣮