Question

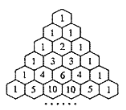
【题目】“杨辉三角”是我国数学史上的一个伟大成就，是二项式系数在三角形中的一种几何排列.如图所示，去除所有为1的项，依此构成数列2，3，3，4，6，4，5，10，10，5，…，则此数列的前46项和为_____.

Answer 1

【答案】

【解析】

根据“杨辉三角”的特点可知次二项式的二项式系数对应“杨辉三角”中的第行，从而得到第行去掉所有为的项的各项之和为：；根据每一行去掉所有为的项的数字个数成等差数列的特点可求得至第行结束，数列共有项，则第项为，从而加和可得结果.

由题意可知，次二项式的二项式系数对应“杨辉三角”中的第行

则“杨辉三角”第行各项之和为：

第行去掉所有为的项的各项之和为：

从第行开始每一行去掉所有为的项的数字个数为：

则：，即至第行结束，数列共有项

第项为第行第个不为的数，即为：

前项的和为：

本题正确结果：