题目内容
已知圆的圆心C在直线y=-2x上,且与直线x+y-1=0相切于点A(2,-1)(1)求圆C的方程
(2)经过点B(8,-3)的一束光线射到T(t,0)后被x轴反射,反射光线与圆C有公共点,求实数t的取值范围.
【答案】分析:(1)设圆C的方程为(x-a)2+(y-b)2=r2,可得圆心C(a,b),把圆心C坐标代入y=-2x得到关于a与b的方程,再由切点A在圆上,把A的坐标代入所设的圆C方程,得到一个关系式,再由切线的性质可得直线AO与切线垂直,由切线的斜率,根据两直线垂直时斜率的乘积为-1,得出关于a与b的另一个方程,把两个关于a与b的方程联立组成方程组,求出方程的解集得到a与b的值,再把求出的a与b的值代入关系式中求出r2,即可确定出圆C的方程;
(2)求出B关系x轴的对称点B′,设反射线方程的斜率为k,表示出反射线的方程,记作(ξ),当该直线与圆C相切时,圆心到直线的距离等于圆的半径,故利用点到直线的距离公式列出关于k的方程,求出方程的解得到k的两个值,可得出光的反射线与圆C有公共点时k的范围,把反射点T的坐标代入(ξ)中,用k表示出t,根据此时函数为增函数,由k的范围即可求出t的范围.
解答:解:(1)设圆C的方程为(x-a)2+(y-b)2=r2,
根据题意得: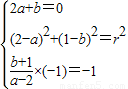 ,
,
解得: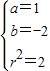 ,
,
则圆C的方程为(x-1)2+(y+2)2=2;
(2)易知点B(8,-3)关于x轴的对称点为B′(8,3),
则设光的反射线方程为y-3=k(x-8),即kx-y+3-8k=0(ξ),
若该直线与圆C相切,则有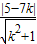 =
=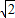 ,
,
解得:k=1或k=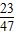 ,
,
则当光的反射线与圆有公共点时,k∈[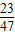 ,1],
,1],
将T(t,0)代入(ξ)中得:t=8-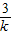 ,
,
该函数在[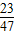 ,1]上是增函数,
,1]上是增函数,
则实数t的范围是[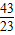 ,5].
,5].
点评:此题考查了直线与圆的位置关系,涉及的知识有:点到直线的距离公式,圆的标准方程,两直线垂直时斜率满足的关系,关于坐标轴对称的点的特点,切线的性质,以及函数增减性的运用,当直线与圆相切时,圆心到直线的距离等于圆的半径,熟练掌握此性质是解本题的关键.
(2)求出B关系x轴的对称点B′,设反射线方程的斜率为k,表示出反射线的方程,记作(ξ),当该直线与圆C相切时,圆心到直线的距离等于圆的半径,故利用点到直线的距离公式列出关于k的方程,求出方程的解得到k的两个值,可得出光的反射线与圆C有公共点时k的范围,把反射点T的坐标代入(ξ)中,用k表示出t,根据此时函数为增函数,由k的范围即可求出t的范围.
解答:解:(1)设圆C的方程为(x-a)2+(y-b)2=r2,
根据题意得:
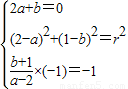 ,
,解得:
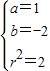 ,
,则圆C的方程为(x-1)2+(y+2)2=2;
(2)易知点B(8,-3)关于x轴的对称点为B′(8,3),
则设光的反射线方程为y-3=k(x-8),即kx-y+3-8k=0(ξ),
若该直线与圆C相切,则有
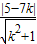 =
=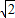 ,
,解得:k=1或k=
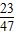 ,
,则当光的反射线与圆有公共点时,k∈[
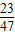 ,1],
,1],将T(t,0)代入(ξ)中得:t=8-
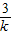 ,
,该函数在[
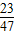 ,1]上是增函数,
,1]上是增函数,则实数t的范围是[
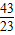 ,5].
,5].点评:此题考查了直线与圆的位置关系,涉及的知识有:点到直线的距离公式,圆的标准方程,两直线垂直时斜率满足的关系,关于坐标轴对称的点的特点,切线的性质,以及函数增减性的运用,当直线与圆相切时,圆心到直线的距离等于圆的半径,熟练掌握此性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目