题目内容
已知半径为2的圆的圆心C在x轴上,圆心C的横坐标是非负整数,且与直线4x+3y+10=0相切.
(Ⅰ)求圆C的方程;
(Ⅱ)设直线l:y=kx+1与圆相交于P、Q两点,若
•
=-2,求k的值;
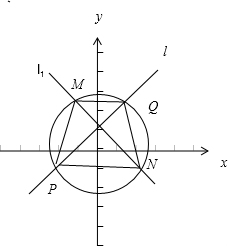
(Ⅲ)已知直线l:y=kx+1,过点(0,1)作直线l1与l垂直,且直线l1与圆C交于M、N两点,求四边形PQMN面积的最大值.
(Ⅰ)求圆C的方程;
(Ⅱ)设直线l:y=kx+1与圆相交于P、Q两点,若
| OP |
| OQ |
(Ⅲ)已知直线l:y=kx+1,过点(0,1)作直线l1与l垂直,且直线l1与圆C交于M、N两点,求四边形PQMN面积的最大值.
分析:(Ⅰ)设圆心M的坐标为(m,0),且m是整数,由圆C与已知直线垂直,得到圆心到直线的距离等于圆的半径,利用点到直线的距离公式列出关于m的方程,求出方程的解得到m的值,进而确定出圆C的方程;
(Ⅱ)
•
=-2可求得∠POQ,进而求出圆心到直l:kx-y+1=0的距离,再去求k.
(Ⅲ)设圆心O到直线l,l1的距离分别为d,d1,四边形PMQN的面积S,直线l,l1都经过点(0,1),且l⊥l1,根据题勾股定理,知d12+d2=1,又根据垂径定理和勾股定理,得到|PQ|=2,|MN|=2,由此能求出四边形PMQN面积的大值.
(Ⅱ)
| OP |
| OQ |
(Ⅲ)设圆心O到直线l,l1的距离分别为d,d1,四边形PMQN的面积S,直线l,l1都经过点(0,1),且l⊥l1,根据题勾股定理,知d12+d2=1,又根据垂径定理和勾股定理,得到|PQ|=2,|MN|=2,由此能求出四边形PMQN面积的大值.
解答:解:(1)设圆心为M(m,0)(m∈Z),
∵圆C与直线4x+3y+10=0相切,且半径为2,
∴圆心,到直线4x+3y+10=0的距离d=r,即
=2,即|4m+10|=10,
∵m圆心C的横坐标是非负整数,∴m=0,
则所求圆的方程为x2+y2=4;
(Ⅱ)因为,
•
=2×2cos<
,
>=-2,
所以,COS∠POQ=-
,∠POQ=120°,
所以圆心到直l:kx-y+1=0的距离d=1,d=
,所以 k=0.
(Ⅲ)设圆心O到直线l,l1的距离分别为d,d1,
四边形PMQN的面积S,
∵直线l,l1都经过点(0,1),且l⊥l1,
根据题勾股定理,知d12+d2=1,
又根据垂径定理和勾股定理,得到
|PQ|=2
,|MN|=2
,
而S=
|PQ|•|MN|,
即S=
×2×
×2×
=2
=2
≤2
=2
=7.
当且仅当d1=d时,等号成立,
所以S的最大值为7.
∵圆C与直线4x+3y+10=0相切,且半径为2,
∴圆心,到直线4x+3y+10=0的距离d=r,即
| |4m+10| |
| 5 |
∵m圆心C的横坐标是非负整数,∴m=0,
则所求圆的方程为x2+y2=4;
(Ⅱ)因为,
| OP |
| OQ |
| OP |
| OQ |
所以,COS∠POQ=-
| 1 |
| 2 |
所以圆心到直l:kx-y+1=0的距离d=1,d=
| 1 | ||
|
(Ⅲ)设圆心O到直线l,l1的距离分别为d,d1,
四边形PMQN的面积S,
∵直线l,l1都经过点(0,1),且l⊥l1,

根据题勾股定理,知d12+d2=1,
又根据垂径定理和勾股定理,得到
|PQ|=2
| 4-d 2 |
| 4-d12 |
而S=
| 1 |
| 2 |
即S=
| 1 |
| 2 |
| 4-d 2 |
| 4-d12 |
=2
| 16-4(d2+d12)+d2d12 |
| 12+d2d12 |
≤2
12+(
|
=2
12+
|
=7.
当且仅当d1=d时,等号成立,
所以S的最大值为7.
点评:此题考查了直线与圆相交的性质,以及直线与圆的位置关系,涉及的知识有:点到直线的距离公式,一元二次方程根的判别式与解的关系,一元二次不等式的解法,解题的关键是:当直线与圆相切时,圆心到直线的距离等于圆的半径;将直线与圆的方程联立消去y后,得到关于x的一元二次方程,此一元二次方程的解的个数决定了直线与圆交点的个数.与圆有关的比例线段,是中档题.解题时要认真审题,注意垂径定理和勾股定理的灵活运用.

练习册系列答案
相关题目
 •
• =-2,求k的值;
=-2,求k的值;