题目内容
已知函数f(x)=|x|-cosx+1,对于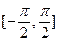 上的任意x1、x2,有如下条件:①x1>x2;②|x1|>|x2|;③x13>x23;④x12>x22;⑤|x1|>x2,其中能使f(x1)>f(x2)恒成立的条件的序号是 ;
上的任意x1、x2,有如下条件:①x1>x2;②|x1|>|x2|;③x13>x23;④x12>x22;⑤|x1|>x2,其中能使f(x1)>f(x2)恒成立的条件的序号是 ;
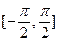 上的任意x1、x2,有如下条件:①x1>x2;②|x1|>|x2|;③x13>x23;④x12>x22;⑤|x1|>x2,其中能使f(x1)>f(x2)恒成立的条件的序号是 ;
上的任意x1、x2,有如下条件:①x1>x2;②|x1|>|x2|;③x13>x23;④x12>x22;⑤|x1|>x2,其中能使f(x1)>f(x2)恒成立的条件的序号是 ;②④
略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
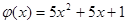
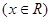 ,函数
,函数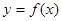 的图象与
的图象与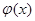 的图象关于点
的图象关于点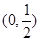 中心对称。
中心对称。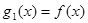 ,
,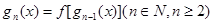 ,试求出使
,试求出使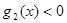 成立的
成立的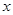 取值范围;
取值范围;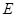 ,使
,使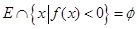 对于区间内的任意实数
对于区间内的任意实数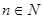 且
且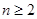 时,都有
时,都有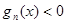 恒成立?
恒成立?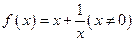 。
。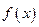 的奇偶性;
的奇偶性;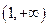 上的单调性;
上的单调性;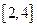 上的最大和最小值。
上的最大和最小值。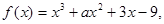 已知
已知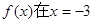 时取得极值,则
时取得极值,则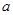 = ( )
= ( )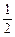 ax2+3x.
ax2+3x.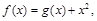 曲线
曲线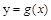 在点
在点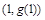 处的切线方程为
处的切线方程为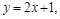 则曲线
则曲线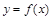 在点
在点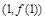 处切线的斜率为( )
处切线的斜率为( )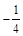
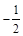
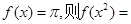 ( )
( ) B.
B.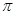 C.
C.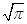 D.不确定
D.不确定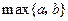 表示a,b两个数中的最大数,设
表示a,b两个数中的最大数,设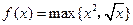
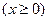 ,那么由函数
,那么由函数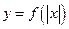 的图象、x轴、直线
的图象、x轴、直线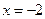 和直线
和直线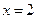 所围成的封闭图形的面积之和是
所围成的封闭图形的面积之和是 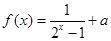 是奇函数,则
是奇函数,则