题目内容
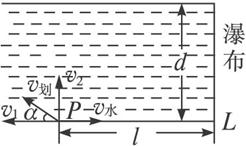
今有一小船位于d=60 m宽的河边P处,从这里起,在下游l=80 m的L处河流变成“飞流直下三千尺”的瀑布.若河水流速方向由上游指向下游(与河岸平行),水速大小为5 m/s,如图所示,为了使小船能安全渡河,船的划速不能小于多少?当划速最小时,划速方向如何?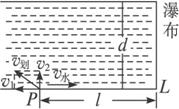
解法一:设船的划速为v划,方向与上游河岸的夹角为α,如下图所示,将v划正交分解为v1,v2,则

v1=v划cosα,v2=v划sinα.
船同时参与两个分运动:一个是沿v2方向的速度为v2的匀速直线运动,另一个是沿v水方向的速度为(v水-v1)的匀速直线运动,这两个分运动的时间t1和t2必相等.设船到达对岸时,极其靠近河流与瀑布的交界处.
由t1=![]() ,t2=
,t2=![]() ,
,
可得![]() =
=![]() ,
,
即![]() =
=![]() ,注意到d=60 m,l=80 m,v水=5 m/s,
,注意到d=60 m,l=80 m,v水=5 m/s,
有![]() =
=![]() ,
,
∴v划=![]() .
.
令y=3cosα+4sinα=5(![]() )
)
=5sin(α+β),其中tanβ=![]() ,β≈37°.
,β≈37°.
显见,当sin(α+β)=1时,ymax=5,v划有最小值为3 m/s.
此时α=90°-37°=53°.
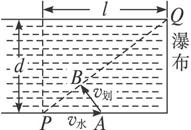
解法二:在题设条件下,船的临界合速度沿下图中的PQ方向,设PA=v水,从A向PQ作垂线,垂足为B,有向AB即表示最小划速的大小和方向,v划最小=v水sinθ,
而sinθ=![]() =
=![]()
=![]() =0.6(θ=37°),
=0.6(θ=37°),
故(v划)min=5×0.6=3(m/s),划速方向与解法一相同.

练习册系列答案
相关题目
 r
r