题目内容
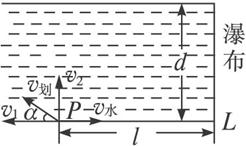
今有一小船位于d=60m宽的河边P处,从这里起,在下游l=80m处河流有一瀑布,若河水流速方向由上游指向下游(与河岸平行).水速大小为5m/s,如图,为了使小船能安全渡河,船的划速不能小于多少?当划速最小时,划速方向如何?

答案:略
解析:
提示:
解析:
|
解法 1:如图,由题设可知,船的实际速度 ,其方向为临界方向 ,其方向为临界方向 ,则最小划速 ,则最小划速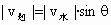 , ,
∴q =37°. ∴最小划速应为 解法2:该船的划速为
令y=3cos a +4sin a =5sin(a +b ).
∴当 sin(a +b )=1时, , ,
∴ 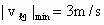 . .
此时a =90°-37°=53°.故船的划速不能小于 3m/s,小船才能安全过河,此时船的划速与上游河岸的夹角为53°.解答本题的关键在于运用向量的观点将物理问题转化为数学问题,并建立相应的数学模型,这也将是今后能力培养的主要方面. |
提示:
|
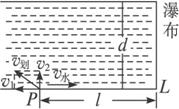
解法 1是按向量的平行四边形法则求合速度,解法2是利用向量的正交分解求解,将划速 分解为河流方向与垂直于河岸方向的两个分速度求解.用到了向量的基本定理及三角函数等知识,两种方法各具特色. 分解为河流方向与垂直于河岸方向的两个分速度求解.用到了向量的基本定理及三角函数等知识,两种方法各具特色. |

练习册系列答案
相关题目

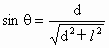
 ,
, .
.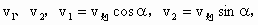 由物理学知识可知
由物理学知识可知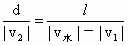 ,∴
,∴ .
.
 r
r