题目内容
在△ABC中,中线长AM=2.

(1)若 =-2
=-2 ,求证:
,求证: +
+ +
+ =0;
=0;
(2)若P为中线AM上的一个动点,求 ·(
·( +
+ )的最小值.
)的最小值.

(1)若
 =-2
=-2 ,求证:
,求证: +
+ +
+ =0;
=0;(2)若P为中线AM上的一个动点,求
 ·(
·( +
+ )的最小值.
)的最小值.(1)见解析;(2)最小值-2.
试题分析:(1) ∵M是BC的中点,∴
 =
= (
( +
+ ).代入
).代入 =-2
=-2 ,得
,得 =-
=- -
- ,即
,即 +
+ +
+ =0
=0 (2)若P为中线AM上的一个动点,若AM=2,我们易将
 ·(
·( +
+ ),转化为-2|
),转化为-2| ||
|| |=2(x-1)2-2的形式,然后根据二次函数在定区间上的最值的求法,得到答案.
|=2(x-1)2-2的形式,然后根据二次函数在定区间上的最值的求法,得到答案.试题解析:(1)证明:∵M是BC的中点,
∴
 =
= (
( +
+ ) ..3分
) ..3分代入
 =-2
=-2 ,得
,得 =-
=- -
- , .2分
, .2分即
 +
+ +
+ =0 1分
=0 1分(2)设|
 |=x,则|
|=x,则| |=2-x(0≤x≤2) .1分
|=2-x(0≤x≤2) .1分∵M是BC的中点,∴
 +
+ =2
=2 2分
2分∴
 ·(
·( +
+ )=2
)=2 ·
· =-2|
=-2| ||
|| |
|=-2x(2-x)=2(x2-2x)=2(x-1)2-2, 2分
当x=1时,取最小值-2 ..1分

练习册系列答案
相关题目
 △ABC的面积
△ABC的面积 夹角的取值范围是( )
夹角的取值范围是( )

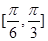





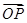 ·
·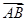 的最小值为________.
的最小值为________. 、
、 ,满足
,满足 ,
, ,则
,则 .
. 与
与 的夹角为
的夹角为 ,
,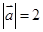 ,
, ,则
,则 =( )
=( )

 中,
中,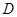 为
为 的中点,且
的中点,且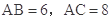 ,则
,则 的值为
的值为



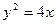 的焦点,A是抛物线上一点,若
的焦点,A是抛物线上一点,若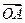 ·
·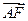 =
=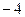 ,则点A的坐标是 ( )
,则点A的坐标是 ( )


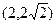
 且
且 则
则 与
与 的夹角为 。
的夹角为 。