题目内容
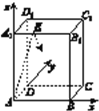
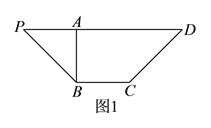
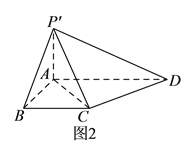
【题目】如图,AB为圆O的直径,点E、F在圆O上,AB ∥EF,矩形ABCD所在平面与圆O所在的平面互相垂直.已知AB=2,EF=1.
(1)求证:平面DAF⊥平面CBF;
(2)求直线AB与平面CBF所成角的大小;
(3)求AD的长为何值时,平面DFC与平面FCB所成的锐二面角的大小为60°?

【答案】(1)详见解析(2)∠ABF=30°.(3)![]() .
.
【解析】试题分析:(1)利用面面垂直的性质,可得CB⊥平面ABEF,再利用线面垂直的判定,证明AF⊥平面CBF,从而利用面面垂直的判定可得平面DAF⊥平面CBF;(2)确定∠ABF为直线AB与平面CBF所成的角,过点F作FH⊥AB,交AB于H,计算出AF,即可求得直线AB与平面CBF所成角的大小;(3)建立空间直角坐标系,求出平面DCF的法向量![]() 平面CBF的一个法向量
平面CBF的一个法向量 利用向量的夹角公式,即可求得AD的长.
利用向量的夹角公式,即可求得AD的长.
试题解析:
(1)∵平面ABCD⊥平面ABEF,CB⊥AB,
平面ABCD∩平面ABEF=AB,∴CB⊥平面ABEF.
∵AF平面ABEF,∴AF⊥CB,
又∵AB为圆O的直径,
∴AF⊥BF,CB∩BF=B,CB,BF平面CBF,
∴AF⊥平面CBF.
∵AF平面ADF,∴平面DAF⊥平面CBF.
(2)由(1)知,AF⊥平面CBF,
∴FB为AB在平面CBF内的射影,
∴∠ABF为直线AB与平面CBF所成的角.
∵AB∥EF,∴四边形ABEF为等腰梯形.
过点F作FH⊥AB,交AB于H.
AB=2,EF=1,则AH=![]() =
=![]() .
.
在Rt△AFB中,根据射影定理AF2=AH·AB,
得AF=1.
sin∠ABF=![]() =
=![]() ,
,
∴∠ABF=30°.

(3)设EF中点为G,以O为坐标原点,OA、OG、AD方向分别为x轴、y轴、z轴方向建立空间直角坐标系(如图).
设AD=t(t>0),则点D的坐标为(1,0,t),
则C(-1,0,t),又A(1,0,0),B(-1,0,0),F(![]() ,
,![]() ,0),
,0),
∴![]() =(2,0,0),
=(2,0,0),![]() =(
=(![]() ,-
,-![]() ,t).
,t).
设平面DFC的平面法向量为n1(x,y,z)
即
令z=![]() ,解得x=0,y=2t.∴n1=(0,2t,
,解得x=0,y=2t.∴n1=(0,2t,![]() ).
).
由(1)可知AF⊥平面CFB,取平面CBF的一个法向量为n2=![]() =(-
=(-![]() ,
,![]() ,0),
,0),
∴cos60°=![]() ,即
,即![]() =
=![]() ,
,
解得t=![]() .
.