题目内容
已知函数 .
.
(Ⅰ)求函数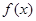 的单调区间;
的单调区间;
(Ⅱ)若 在
在 内恒成立,求实数
内恒成立,求实数 的取值范围.
的取值范围.
(Ⅲ) ,求证:
,求证: .
.
(Ⅰ)当 时,
时,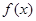 在
在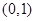 单调递减,在
单调递减,在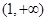 上单调递增;
上单调递增;
当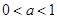 时,
时,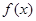 在
在 单调递减,在
单调递减,在 ,
,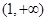 上单调递增;
上单调递增;
当 时,
时,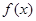 在
在 上单调递增;
上单调递增;
当 时,
时,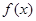 在
在 单调递减, 在
单调递减, 在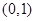 ,
, 上单调递增;
上单调递增;
(Ⅱ)
(Ⅲ)详见解析
解析试题分析:(Ⅰ)利用导数的符号确定函数的单调区间。函数含有参数,故需要分情况讨论.
(Ⅱ)思路一、一般地若任意 使得
使得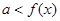 ,则
,则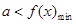 ;若任意
;若任意 使得
使得 ,则
,则 .由
.由 得:
得: 恒成立,所以
恒成立,所以 小于等于
小于等于 的最小值.
的最小值.
思路二、除 外,
外, 是
是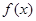 的一个极值点,故可首先考虑
的一个极值点,故可首先考虑 这个特殊值.由
这个特殊值.由 得:
得:  ,这样只需考虑
,这样只需考虑 时
时 在
在 内是否恒成立.这是本题的特点,需要仔细观察、分析.若发现其特点,则运算大大简化.所以这个题有较好的区分度.
内是否恒成立.这是本题的特点,需要仔细观察、分析.若发现其特点,则运算大大简化.所以这个题有较好的区分度.
(Ⅲ)涉及数列求和的不等式的证明,一般有两种类型,一种是先求和,后放缩;一种先放缩,后求和.
本题显然属于后者.
解答题中的最后一问,往往要用前面的结论,本题也不例外.由(Ⅱ)取 可得:
可得: ,由此可将不等式左边各项放缩.
,由此可将不等式左边各项放缩.
但是如果第一项也用这个结论来放缩,则得不到右边的式子.这时就考虑从第二项开始,或从第三项开始用这个结论.
试题解析:(Ⅰ)
当 时,
时,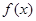 在
在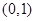 单调递减,在
单调递减,在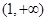 上单调递增;
上单调递增;
当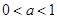 时,
时,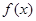 在
在 单调递减,在
单调递减,在 ,
,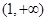 上单调递增;
上单调递增;
当 时,
时,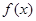 在
在 上单调递增;
上单调递增;
当 时,
时,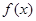 在
在 单调递减, 在
单调递减, 在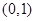 ,
, 上单调递增.
上单调递增.
(Ⅱ)法一、由 得:
得:
令 ,则
,则
令 ,则
,则 即
即
所以由 得
得
所以 在
在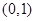 内单调递减,在
内单调递减,在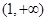 内单调递增.所以
内单调递增.所以
从而
法二、由 得:
得: 
又 时,
时, 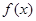 在
在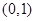 单调递减,在
单调递减,在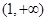 上单调递增
上单调递增
所以即: 
所以若 在
在 内恒成立,实数
内恒成立,实数 的取值范围为
的取值范围为 .
.
(Ⅲ)由(Ⅱ)知: 又 时,
时,  即
即 (
( 时取等号)
时取等号)
所以当 时:
时: 
又 ,所以
,所以 .
.
考点:本题考查函数的导数、导数的应用及不等式的证明.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目

 为函数
为函数 的极值点,求证:
的极值点,求证:  ;
; 时,
时, 恒成立,求正整数
恒成立,求正整数 的最大值.
的最大值. ,设曲线
,设曲线 在与
在与 轴交点处的切线为
轴交点处的切线为 ,
, 为
为 的导函数,满足
的导函数,满足 .
. ,
, ,求函数
,求函数 在
在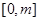 上的最大值;
上的最大值; ,若对于一切
,若对于一切 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛 ,要求
,要求 在
在 的延长线上,
的延长线上, 在
在 的延长线上,且对角线
的延长线上,且对角线 过
过 点.已知
点.已知 米,
米, 米。
米。
 (单位:米),要使花坛
(单位:米),要使花坛 的取值范围;
的取值范围;  (单位:米),则当
(单位:米),则当 ,
, 的长度分别是多少时,花坛
的长度分别是多少时,花坛 ,其中
,其中 .
. 时,记
时,记 存在
存在 使
使 成立,求实数
成立,求实数 的取值范围;
的取值范围; 在
在 上存在最大值和最小值,求
上存在最大值和最小值,求 的取值范围.
的取值范围. (
( R),且该函数曲线
R),且该函数曲线 在
在 处的切线与
处的切线与 轴平行.
轴平行. 的单调性;
的单调性; 时,
时, .
. 是
是 的一个极值点.
的一个极值点. 的值;
的值;  的单调递减区间;
的单调递减区间; ,试问过点
,试问过点 可作多少条直线与曲线
可作多少条直线与曲线 相切?请说明理由.
相切?请说明理由.  .
. 的图象在
的图象在 处的切线斜率为
处的切线斜率为 ,求实数
,求实数 的值;
的值; 在
在 上是减函数,求实数
上是减函数,求实数 (
( 为常数),且
为常数),且 在点
在点 处的切线平行于
处的切线平行于 轴.
轴.