题目内容
求证:方程x=asinx+b(a>0,b>0)至少有一个正根,且它不大于a+b.
证明略
设f(x)=asinx+b-x,
则f(0)=b>0,f(a+b)=a·sin(a+b)+b-(a+b)=a[sin(a+b)-1]≤0,
又f(x)在(0,a+b]内是连续函数,所以存在一个x0∈(0,a+b],使f(x0)=0,即x0是方程f(x)=0的根,也就是方程x=a·sinx+b的根。
因此,方程x=asinx+b至少存在一个正根,且它不大于a+b。
则f(0)=b>0,f(a+b)=a·sin(a+b)+b-(a+b)=a[sin(a+b)-1]≤0,
又f(x)在(0,a+b]内是连续函数,所以存在一个x0∈(0,a+b],使f(x0)=0,即x0是方程f(x)=0的根,也就是方程x=a·sinx+b的根。
因此,方程x=asinx+b至少存在一个正根,且它不大于a+b。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
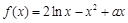 (
(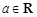 ).
).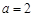 时,求
时,求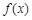 的图象在
的图象在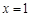 处的切线方程;
处的切线方程;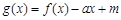 在
在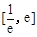 上有两个零点,求实数
上有两个零点,求实数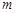 的取值范围;
的取值范围;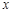 轴有两个不同的交点
轴有两个不同的交点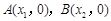 ,且
,且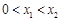 ,求证:
,求证: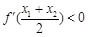 (其中
(其中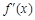 是
是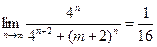 ,求实数m的取值范围.
,求实数m的取值范围.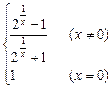
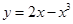 在横坐标为
在横坐标为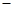 l的点处的切线为
l的点处的切线为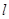 ,则点P(3,2)到直线
,则点P(3,2)到直线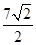
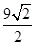
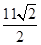
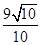
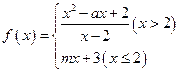 在点
在点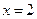 处连续,则
处连续,则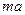 的值是 .
的值是 . 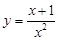 (
(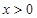 )上横坐标为1的点的切线方程为( )
)上横坐标为1的点的切线方程为( )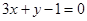
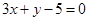


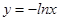 在点
在点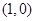 处的切线斜率为 .
处的切线斜率为 .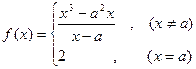 是连续函数,则实数
是连续函数,则实数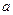 的值是
的值是


