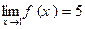题目内容
已知函数f(x)=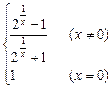
(1)f(x)在x=0处是否连续?说明理由;
(2)讨论f(x)在闭区间[-1,0]和[0,1]上的连续性.
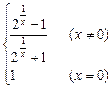
(1)f(x)在x=0处是否连续?说明理由;
(2)讨论f(x)在闭区间[-1,0]和[0,1]上的连续性.
(1) f(x)在x=0处不连续(2) f(x)在[-1,0]上是不连续函数,在[0,1]上是连续函数.
f(x)=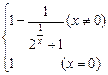
(1)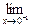 f(x)=-1,
f(x)=-1,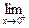 f(x)=1,所以
f(x)=1,所以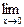 f(x)不存在,
f(x)不存在,
故f(x)在x=0处不连续.
(2)f(x)在(-∞,+∞)上除x=0外,再无间断点,
由(1)知f(x)在x=0处右连续,
所以f(x)在[-1,0]上是不连续函数,在[0,1]上是连续函数.
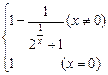
(1)
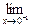 f(x)=-1,
f(x)=-1,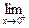 f(x)=1,所以
f(x)=1,所以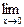 f(x)不存在,
f(x)不存在,故f(x)在x=0处不连续.
(2)f(x)在(-∞,+∞)上除x=0外,再无间断点,
由(1)知f(x)在x=0处右连续,
所以f(x)在[-1,0]上是不连续函数,在[0,1]上是连续函数.

练习册系列答案
相关题目
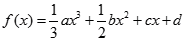 的图像过原点,且在点
的图像过原点,且在点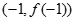 处的切线与
处的切线与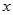 轴平行,对任意
轴平行,对任意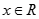 ,都有
,都有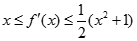 .
.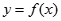 在点
在点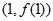 处切线的斜率;
处切线的斜率;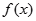 的解析式;
的解析式;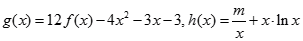 ,对任意
,对任意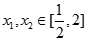 ,都有
,都有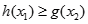 .求实数
.求实数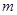 的取值范围.
的取值范围.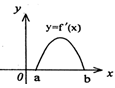
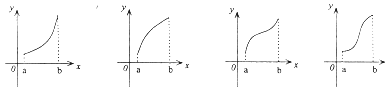
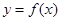 是定义在R上的可导函数,则下列说法不正确的是( )
是定义在R上的可导函数,则下列说法不正确的是( )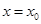 时取得极值,则
时取得极值,则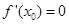
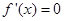 ,则
,则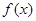 在
在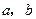 的值,使
的值,使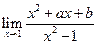 与
与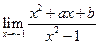 都是有限的.
都是有限的.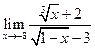 的值.
的值.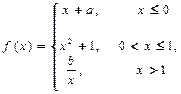 在定义域内连续,则
在定义域内连续,则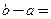
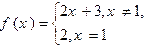 ,则下面结论错误的个数是( )
,则下面结论错误的个数是( )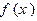 在
在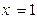 处连续 (2)
处连续 (2)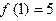 (3)
(3)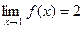 (4)
(4)