题目内容
如果椭圆 的弦被点(4,2)平分,则这条弦所在的直线方程是 ( )
的弦被点(4,2)平分,则这条弦所在的直线方程是 ( )
A. | B. | C. | D. |
D
解析试题分析:设这条弦的两端点为A(x1,y1),B(x2,y2),斜率为k,则 ,两式相减再变形得
,两式相减再变形得 又弦中点为(4,2),故k=?
又弦中点为(4,2),故k=?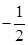 ,故这条弦所在的直线方程y-2=?
,故这条弦所在的直线方程y-2=? (x-4),整理得x+2y-8=0;故选D..
(x-4),整理得x+2y-8=0;故选D..
考点:椭圆的应用;直线与圆锥曲线的综合问题..

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
抛物线 上一点
上一点 到直线
到直线 的距离与到点
的距离与到点 的距离之差的最大值为( )
的距离之差的最大值为( )
A. | B.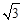 | C. | D. |
已知双曲线 与椭圆
与椭圆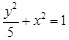 有相同的焦点,则该双曲线的渐近线方程为( )
有相同的焦点,则该双曲线的渐近线方程为( )
A. | B. | C. | D. |
抛物线 的焦点坐标是( )
的焦点坐标是( )
A. | B. | C.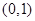 | D. |
过抛物线y2=8x的焦点F作倾斜角为135°的直线交抛物线于A,B两点,则弦AB的长为( )
| A.4 | B.8 | C.12 | D.16 |
椭圆 =1的焦点为F1和F2,点P在椭圆上,如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的( )
=1的焦点为F1和F2,点P在椭圆上,如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的( )
| A.7倍 | B.5倍 | C.4倍 | D.3倍 |
若抛物线 的焦点是双曲线
的焦点是双曲线 的一个焦点,则正数
的一个焦点,则正数 等于( )
等于( )
A. | B. | C. | D. |
 :
:  与双曲线
与双曲线 的公共焦点A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )
的公共焦点A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )
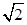 B.
B. C.
C. D.
D.

