题目内容
 (2012•宝鸡模拟)如图,已知PA⊥平面ABC,且PA=
(2012•宝鸡模拟)如图,已知PA⊥平面ABC,且PA=| 2 |
(1)求证:PC⊥平面ADE;
(2)求点D到平面ABC的距离.
分析:(1)利用线面垂直的性质与判定,证明PC⊥平面ADE,证出PC⊥AD,PC⊥AE即可;
(2)过D点作DF⊥BA垂直为E,由题意知DF⊥面ABC,即DF为所求距离,利用三角形的相似,可得结论.
(2)过D点作DF⊥BA垂直为E,由题意知DF⊥面ABC,即DF为所求距离,利用三角形的相似,可得结论.
解答:(1)证明:因为PA⊥平面ABC,所以PA⊥BC,
又AB⊥BC,且PA∩AB=A,所以BC⊥平面PAB,
因为AD?平面PAB,所以BC⊥AD.…(3分)
又AD⊥PB,BC∩PB=B,所以AD⊥平面PBC,
因为PC?平面PBC,所以PC⊥AD,
又PC⊥AE,AD∩AE=A,所以PC⊥平面ADE.…(6分)
(2)解:过D点作DF⊥BA垂直为E,
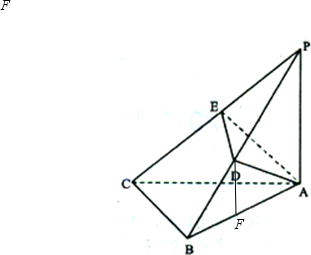
由题意知DF⊥面ABC,即DF为所求距离.…(8分)
由题设得DF∥PA,所以△BDE∽△BAP,即DF=
,
又∵△BDA∽△BAP,∴
=
即BD=
=
,∴BD=
PB.
∴DF=
.…(11分)
即点D到平面ABC的距离为
.…(12分)
又AB⊥BC,且PA∩AB=A,所以BC⊥平面PAB,
因为AD?平面PAB,所以BC⊥AD.…(3分)
又AD⊥PB,BC∩PB=B,所以AD⊥平面PBC,
因为PC?平面PBC,所以PC⊥AD,
又PC⊥AE,AD∩AE=A,所以PC⊥平面ADE.…(6分)
(2)解:过D点作DF⊥BA垂直为E,

由题意知DF⊥面ABC,即DF为所求距离.…(8分)
由题设得DF∥PA,所以△BDE∽△BAP,即DF=
| BD•PA |
| PB |
又∵△BDA∽△BAP,∴
| BD |
| AB |
| AB |
| PB |
即BD=
| AB2 |
| PB |
| ||
| 3 |
| 1 |
| 3 |
∴DF=
| ||
| 3 |
即点D到平面ABC的距离为
| ||
| 3 |
点评:本题考查线面垂直的性质与判定,考查点到面的距离,掌握线面垂直的性质与判定,作出点到面的距离的线段是关键.

练习册系列答案
相关题目
 (2012•宝鸡模拟)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
(2012•宝鸡模拟)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<