题目内容
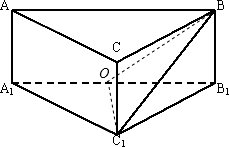
 如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是( )
如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是( )分析:取A1B1的中点O,连接OB,则可得∠C1BO是BC1与平面AB B1 A1所成角,由此可得结论.
解答:解:取A1B1的中点O,连接OB,则
∵AC=BC=2,∴C1O⊥A1B1,C1O=
∵ABC-A1 B1 C1为直三棱柱,∴C1O⊥平面AB B1 A1,
∴∠C1BO是BC1与平面AB B1 A1所成角
∵AA1=1,∴BC1=
∴sin∠C1BO=
=
=
故选D.

∵AC=BC=2,∴C1O⊥A1B1,C1O=
| 2 |
∵ABC-A1 B1 C1为直三棱柱,∴C1O⊥平面AB B1 A1,
∴∠C1BO是BC1与平面AB B1 A1所成角
∵AA1=1,∴BC1=
| 5 |
∴sin∠C1BO=
| C1O |
| BC1 |
| ||
|
| ||
| 5 |
故选D.
点评:本题考查线面角,考查学生的计算能力,正确作出线面角是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




