题目内容

对于实数x，[x]称为取整函数或高斯函数，亦即[x]是不超过x的最大整数．例如：[2.3]．直角坐标平面内，若（x，y）满足[x-1]2+[y-1]2=4，则 x2+y2的取值范围是
[1，5）∪[10，20）
[1，5）∪[10，20）
．
分析：先根据[x]的意义，得出x，y满足
-2≤x-1＜-1或2≤x-1＜3
0≤y-1＜1
或
0≤x-1＜1
-2≤y-1＜-1或2≤y-1＜3
，在平面直角坐标系内画出可行域，再将x2+y2看作可行域内点到坐标原点距离的平方，考察出最值情况，求出范围．
解答：解：由[x-1]2+[y-1]2=4，得
[x-1]=±2
[y-1]=0
 或
[x-1]=0
[y-1]=±2

即
-2≤x-1＜-1或2≤x-1＜3
0≤y-1＜1
或
0≤x-1＜1
-2≤y-1＜-1或2≤y-1＜3

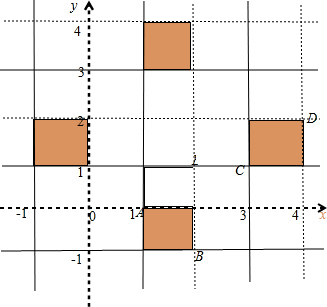表示的可行域如图，且关于y=x对称．
x2+y2看作可行域内点到坐标原点距离的平方．AO2=1，BO2=5此时x2+y2∈[1，5）．CO2=10，DO2=20，
此时x2+y2∈[10，20）．
所以 x2+y2∈[1，5）∪[10，20）．
故答案为：[1，5）∪[10，20）．
点评：本题考查取整函数的意义，数形结合的思想方法，考查了阅读理解、转化、计算能力．
练习册系列答案
相关题目
对于函数f1（x），f2（x），h（x），如果存在实数a，b使得h（x）=a•f1（x）+b•f2（x），那么称h（x）为f1（x），f2（x）的生成函数．
（Ⅰ）下面给出两组函数，h（x）是否分别为f1（x），f2（x）的生成函数？并说明理由；
    第一组：f1(x)=sinx，  f2(x)=cosx，  h(x)=sin(x+
π
3
)；
    第二组：f1（x）=x2-x，f2（x）=x2+x+1，h（x）=x2-x+1；
（Ⅱ）设f1(x)=log2x，  f2(x)=log
1
2
x，  a=2，  b=1，生成函数h（x）．若不等式3h2（x）+2h（x）+t＜0在x∈[2，4]上有解，求实数t的取值范围；
（Ⅲ）设f1(x)=x，   f2(x)=
1
x
   (1≤x≤10)，取a=1，b＞0，生成函数h（x）使h（x）≥b恒成立，求b的取值范围．
对于定义在D上的函数y=f（x），若同时满足．
①存在闭区间[a，b]⊆D，使得任取x1∈[a，b]，都有f（x1）=c （c是常数）；
②对于D内任意x2，当x2∉[a，b]时总有f（x2）＞c称f（x）为“平底型”函数．
（1）（理）判断f1（x）=|x-1|+|x-2|，f2（x）=x+|x-2|是否是“平底型”函数？简要说明理由；
（文）判断f1（x）=|x-1|+|x-2|，f2（x）=x-|x-3|是否是“平底型”函数？简要说明理由；
（2）（理）设f（x）是（1）中的“平底型”函数，若|t-k|+|t+k|≥|k|•f（x），k∈R且k≠0，对一切t∈R恒成立，求实数x的范围；
（文）设f（x）是（1）中的“平底型”函数，若|t-1|+|t+1|≥f（x），对一切t∈R恒成立，求实数x的范围；
（3）（理）若F（x）=mx+
x2+2x+n
，x∈[-2，+∞）是“平底型”函数，求m和n的值；
（文）若F（x）=m|x-1|+n|x-2|是“平底型”函数，求m和n满足的条件．
对于定义在区间D上的函数f（x），若存在闭区间[a，b]⊆D和常数c，使得对任意x1∈[a，b]，都有f（x1）=c，且对任意x2∈D，当x2∉[a，b]时，f（x2）＞c恒成立，则称函数f（x）为区间D上的“平底型”函数．
（1）判断函数f1（x）=|x-1|+|x-2|和f2（x）=x+|x-2|是否为R上的“平底型”函数？并说明理由；
（2）若函数g(x)=x+
x2+2x+n
是区间[-2，+∞）上的“平底型”函数，求n的值．
（3）设f（x）是（1）中的“平底型”函数，k为非零常数，若不等式|t-k|+|t+k|≥|k|•f（x）对一切t∈R恒成立，求实数x的取值范围．
设函数f（x）的定义域为D，若存在非零实数h使得对于任意x∈M（M⊆D），有x+h⊆D，且f（x+h）≥f（x），则称f（x）为M上的“h阶高调函数”．给出如下结论：
①若函数f（x）在R上单调递增，则存在非零实数h使f（x）为R上的“h阶高调函数”；
②若函数f（x）为R上的“h阶高调函数”，则f（x）在R上单调递增；
③若函数f（x）=x2为区间[-1，+∞）上的“h阶高诬蔑财函数”，则h≥2；
④若函数f（x）在R上的奇函数，且x≥0时，f（x）=|x-1|-1，则f（x）只能是R上的“4阶高调函数”．
其中正确结论的序号为（　　）
对于函数f1（x），f2（x），h（x），如果存在实数a，b使得h（x）=a•f1（x）+b•f2（x），那么称h（x）为f1（x），f2（x）的生成函数．
（Ⅰ）下面给出两组函数，h（x）是否分别为f1（x），f2（x）的生成函数？并说明理由；
第一组：f1(x)=sinx，  f2(x)=cosx，  h(x)=sin(x+
π
3
)；
第二组：f1（x）=x2-x，f2（x）=x2+x+1，h（x）=x2-x+1；
（Ⅱ）设f1(x)=log2x，  f2(x)=log
1
2
x，  a=2，  b=1，生成函数h（x）．若不等式3h2（x）+2h（x）+t＜0在x∈[2，4]上有解，求实数t的取值范围；
（Ⅲ）设f1(x)=x，   f2(x)=
1
x
   (1≤x≤10)，取a=1，b＞0，生成函数h（x）使h（x）≥b恒成立，求b的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网