题目内容
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=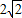 .
.(Ⅰ)求点C到平面PBD的距离.
(Ⅱ)在线段PD上是否存在一点Q,使CQ与平面PBD所成的角的正弦值为
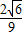 ,若存在,指出点Q的位置,若不存在,说明理由.
,若存在,指出点Q的位置,若不存在,说明理由.
【答案】分析:(I)由已知中,PA⊥平面ABCD,PA=AD=2,BD= ,底面ABCD是矩形,我们易求出棱锥VP-BCD的体积,再根据VP-BCD=VC-PBD,我们只要求出△PBD的面积,然后代入棱锥体积公式,即可求出点C到平面PBD的距离.
,底面ABCD是矩形,我们易求出棱锥VP-BCD的体积,再根据VP-BCD=VC-PBD,我们只要求出△PBD的面积,然后代入棱锥体积公式,即可求出点C到平面PBD的距离.
(II)以A为原点,分别以AB,AD,AP为X,Y,Z轴的正方向建立空间坐标系,则我们易给出各个点的坐标,进而求出CQ的方向向量和平面PBD的法向量,然后根据CQ的方向向量和平面PBD的法向量的夹角的余弦值等于CQ与平面PBD所成的角的正弦值,构造方程,即可求出Q的坐标.
解答: 解:(Ⅰ)在Rt△BAD中,AD=2,BD=
解:(Ⅰ)在Rt△BAD中,AD=2,BD= ,
,
∴AB=2,ABCD为正方形,因此BD⊥AC.(1分)
∵PA=AB=AD=2,∴PB=PD=BD= (2分)
(2分)
设C到面PBD的距离为d,由VP-BCD=VC-PBD,
有 ,
,
即 ,(4分)
,(4分)
得 (5分)
(5分)
(Ⅱ)如图建立空间直角坐标系
因为Q在DP上,所以可设 ,(6分)
,(6分)
又∵ ,
,
∴Q(0,2-2λ,2λ),∴ .(8分)
.(8分)
易求平面PBD的法向量为 ,(10分)
,(10分)
所以设CQ与平面PBD所成的角为θ,则有: =
= (12分)
(12分)
所以有 ,
, ,∵0<λ<1,∴
,∵0<λ<1,∴ (13分)
(13分)
所以存在且 (14分)
(14分)
点评:本题考查的知识点是空间点、线、面的距离计算,及直线与平面所成的解,(I)中利用VP-BCD=VC-PBD,是解答的关键,(II)中求出直线与平面的方向向量和平面的法向量,将线面夹角的正弦值,转化为两个向量的余弦是解答的关键.
 ,底面ABCD是矩形,我们易求出棱锥VP-BCD的体积,再根据VP-BCD=VC-PBD,我们只要求出△PBD的面积,然后代入棱锥体积公式,即可求出点C到平面PBD的距离.
,底面ABCD是矩形,我们易求出棱锥VP-BCD的体积,再根据VP-BCD=VC-PBD,我们只要求出△PBD的面积,然后代入棱锥体积公式,即可求出点C到平面PBD的距离.(II)以A为原点,分别以AB,AD,AP为X,Y,Z轴的正方向建立空间坐标系,则我们易给出各个点的坐标,进而求出CQ的方向向量和平面PBD的法向量,然后根据CQ的方向向量和平面PBD的法向量的夹角的余弦值等于CQ与平面PBD所成的角的正弦值,构造方程,即可求出Q的坐标.
解答:
 解:(Ⅰ)在Rt△BAD中,AD=2,BD=
解:(Ⅰ)在Rt△BAD中,AD=2,BD= ,
,∴AB=2,ABCD为正方形,因此BD⊥AC.(1分)
∵PA=AB=AD=2,∴PB=PD=BD=
 (2分)
(2分)设C到面PBD的距离为d,由VP-BCD=VC-PBD,
有
 ,
,即
 ,(4分)
,(4分)得
 (5分)
(5分)(Ⅱ)如图建立空间直角坐标系
因为Q在DP上,所以可设
 ,(6分)
,(6分)又∵
 ,
,
∴Q(0,2-2λ,2λ),∴
 .(8分)
.(8分)易求平面PBD的法向量为
 ,(10分)
,(10分)所以设CQ与平面PBD所成的角为θ,则有:
 =
= (12分)
(12分)所以有
 ,
, ,∵0<λ<1,∴
,∵0<λ<1,∴ (13分)
(13分)所以存在且
 (14分)
(14分)点评:本题考查的知识点是空间点、线、面的距离计算,及直线与平面所成的解,(I)中利用VP-BCD=VC-PBD,是解答的关键,(II)中求出直线与平面的方向向量和平面的法向量,将线面夹角的正弦值,转化为两个向量的余弦是解答的关键.

练习册系列答案
相关题目
 如图三棱锥P-ABC中,平面PAB⊥平面ABC,AC⊥BC,BC=
如图三棱锥P-ABC中,平面PAB⊥平面ABC,AC⊥BC,BC= 如图三棱锥P-ABC中,△ABC是正三角形,∠PCA=90°,D为PA的中点,二面角P-AC-B为120°,PC=2,AB=
如图三棱锥P-ABC中,△ABC是正三角形,∠PCA=90°,D为PA的中点,二面角P-AC-B为120°,PC=2,AB= 如图三棱锥P-ABC,已知PC⊥平面ABC,CD⊥面PAB,BA=BC,PC=AC=2.
如图三棱锥P-ABC,已知PC⊥平面ABC,CD⊥面PAB,BA=BC,PC=AC=2. 如图三棱锥P-ABC中,△PAC,△ABC是等边三角形.
如图三棱锥P-ABC中,△PAC,△ABC是等边三角形.