题目内容
 如图三棱锥P-ABC中,平面PAB⊥平面ABC,AC⊥BC,BC=
如图三棱锥P-ABC中,平面PAB⊥平面ABC,AC⊥BC,BC=| 3 |
| 3 |
| 2 |
分析:过点P在平面PAB内作PD⊥AB于D,过D点在平面ABC内作DE⊥BC于E,连结PE,可得∠PBC即直线PB与平面ABC所成的角,结合已知可证得∠PED即二面角P-BC-A的平面角,解△ABC,Rt△DBE和Rt△PDE可得答案.
解答: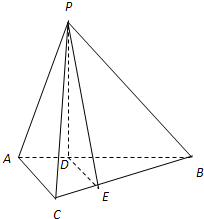 解:过点P在平面PAB内作PD⊥AB于D,过D点在平面ABC内作DE⊥BC于E,连结PE---------------------------------------(2分)
解:过点P在平面PAB内作PD⊥AB于D,过D点在平面ABC内作DE⊥BC于E,连结PE---------------------------------------(2分)
∵平面PAB⊥平面ABC,且平面PAB⊥平面ABC=AB
∴PD⊥平面ABC
∴∠PBC即直线PB与平面ABC所成的角,且PD⊥BC
∴∠PBC=45°---------------------------(4分)
∴在Rt△PDB中,由PB=3
得:PD=BD=3
又∵DE⊥BC,且PD⊥BC
∴BC⊥平面PDE
∴BC⊥PE
∴∠PED即二面角P-BC-A的平面角,------------------(8分)
又∵△ABC中,AC⊥CB,BC=
AC=2
知,∠CBA=30°
∴在Rt△DBE中:DE=
BD=
.
∴在Rt△PDE中:tan∠PDE=
=
=2,
即二面角P-BC-A的正切值为2.----------(12分)
 解:过点P在平面PAB内作PD⊥AB于D,过D点在平面ABC内作DE⊥BC于E,连结PE---------------------------------------(2分)
解:过点P在平面PAB内作PD⊥AB于D,过D点在平面ABC内作DE⊥BC于E,连结PE---------------------------------------(2分)∵平面PAB⊥平面ABC,且平面PAB⊥平面ABC=AB
∴PD⊥平面ABC
∴∠PBC即直线PB与平面ABC所成的角,且PD⊥BC
∴∠PBC=45°---------------------------(4分)
∴在Rt△PDB中,由PB=3
| 2 |
又∵DE⊥BC,且PD⊥BC
∴BC⊥平面PDE
∴BC⊥PE
∴∠PED即二面角P-BC-A的平面角,------------------(8分)
又∵△ABC中,AC⊥CB,BC=
| 3 |
| 3 |
∴在Rt△DBE中:DE=
| 1 |
| 2 |
| 3 |
| 2 |
∴在Rt△PDE中:tan∠PDE=
| PD |
| DE |
| 3 | ||
|
即二面角P-BC-A的正切值为2.----------(12分)
点评:本题考查的知识点是二面角的平面角及其求法,其中证得∠PED即二面角P-BC-A的平面角,将求空间二面角问题转化为解三角形问题是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图三棱锥P-ABC中,△ABC是正三角形,∠PCA=90°,D为PA的中点,二面角P-AC-B为120°,PC=2,AB=
如图三棱锥P-ABC中,△ABC是正三角形,∠PCA=90°,D为PA的中点,二面角P-AC-B为120°,PC=2,AB= 如图三棱锥P-ABC,已知PC⊥平面ABC,CD⊥面PAB,BA=BC,PC=AC=2.
如图三棱锥P-ABC,已知PC⊥平面ABC,CD⊥面PAB,BA=BC,PC=AC=2. 如图三棱锥P-ABC中,△PAC,△ABC是等边三角形.
如图三棱锥P-ABC中,△PAC,△ABC是等边三角形.