Question

如图三棱锥P-ABC，已知PC⊥平面ABC，CD⊥面PAB，BA=BC，PC=AC=2．
（Ⅰ）求异面直线AP与BC所成的角的大小；
（Ⅱ）求二面角C-PA-B的余弦值．

Answer 1

分析：（Ⅰ）先根据PC⊥平面ABC，CD⊥面PAB，BA=BC，PC=AC=2求出BC，再建立空间直角坐标系求出个对应点的坐标；进而求出

AP

，

BC

的坐标，最后直接代入两向量夹角的计算公式即可；（Ⅱ）先根据条件求出平面PAB的法向量以及平面PAC的法向量的坐标，最后计算出其数量积进而求出二面角C-PA-B的余弦值

解答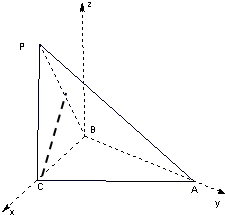：解：（Ⅰ）∵PC⊥平面ABC，∴PC⊥AB．
又∵CD⊥面PAB，
∴CD⊥AB．PC∩PD=P，
∴AB⊥面PCB．∴AB⊥BC．…（2分）
∵PC=AC=2，∴BC=

2

．
以B为原点，建立如图所示的空间直角坐标系，
则A(0，

2

，0)，B(0，0，0)，C(

2

，0，0)，P(

2

，0，2)．

AP

=(

2

，-

2

，2)，

BC

=(

2

，0，0)．

AP

•

BC

=

2

×

2

+0+0=2．
设AP与BC所成的角为θ，cosθ=|

AP • BC

| AP || BC |

|=

2

2× 2 × 2

=

1

2

∴异面直线AP与BC所成的角为

π

3

．…（6分）
（Ⅱ）设平面PAB的法向量为m=(x，y，z).

AB

=(0，-

2

，0)，

AB

=(

2

，-

2

，2)．
∴

AB •m=0 AP •m=0.

∴

- 2 y=0 2 x- 2 y+2z=0.

∴

y=0 x=- 2 z.

令z=-1，∴m=(

2

，0，-1)．…（8分）
设平面PAC的法向量为n=(a，b，c)，

PC

=(0，0，-2)，

AC

=(

2

，-

2

，0)．
∴

PC •n=0 AC •n=0.

∴

-2c=0 2 a- 2 b=0.

∴

c=0 a=b.

令a=1，∴n=（1，1，0）．…（10分）
∴cos＜m，n＞=

m•n

|m||n|

=

2

3 × 2

=

3

3

…（11分）
∴二面角C-PA-B大小的余弦值为

3

3

．…（12分）

点评：本题主要考察用空间向量求平面间的夹角以及异面直线及其所成的角．解决这类题目的关键在于建立适当的坐标系，进而求出对应向量的坐标．