题目内容
 箱中有3个黑球,6个白球,每个球被取到的概率相同,
箱中有3个黑球,6个白球,每个球被取到的概率相同, 箱中没有球.我们把从
箱中没有球.我们把从 箱中取1个球放入
箱中取1个球放入 箱中,然后在
箱中,然后在 箱中补上1个与取走的球完全相同的球,称为一次操作,这样进行三次操作.
箱中补上1个与取走的球完全相同的球,称为一次操作,这样进行三次操作.(1)分别求
 箱中恰有1个、2个、3个白球的概率;
箱中恰有1个、2个、3个白球的概率;(2)从
 箱中一次取出2个球,记白球的个数为
箱中一次取出2个球,记白球的个数为 ,求
,求 的分布列与数学期望.
的分布列与数学期望.(1) 箱中恰有1个、2个、3个白球的概率分别为
箱中恰有1个、2个、3个白球的概率分别为 ;
;
(2)所以 的分布列为
的分布列为

 .
.
 箱中恰有1个、2个、3个白球的概率分别为
箱中恰有1个、2个、3个白球的概率分别为 ;
; (2)所以
 的分布列为
的分布列为
 .
. 试题分析:(1)
 ;
; 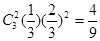 ;
;  ;
;所以
 箱中恰有1个、2个、3个白球的概率分别为
箱中恰有1个、2个、3个白球的概率分别为 ; 6分(每个2分)
; 6分(每个2分)(2)
 ;
; ;
; (或
(或 )
)所以
 的分布列为
的分布列为
12分(每个2分)
 . 14分
. 14分点评:中档题,随机变量的分布列及其数学期望,是近些年来高考重点考查的知识内容,往往以应用题的面目出现,综合考查学习能力,计算能力,阅读理解能力。解题过程中,要注意审清题意,明确算法,细心计算。往往利用排列组合知识,有时借助于“树图法”“坐标法”计算事件数。

练习册系列答案
相关题目
 (件)
(件)

 的分布列与数学期望;
的分布列与数学期望; ,获得50元奖金的概率为
,获得50元奖金的概率为 .
. 、a、a(0<a<1),三人各射击一次,击中目标的次数记为ξ.
、a、a(0<a<1),三人各射击一次,击中目标的次数记为ξ. 成等差数列,则
成等差数列,则 .
.  位,若连续抽取到两位愿意购买本地家禽的市民,或
位,若连续抽取到两位愿意购买本地家禽的市民,或 道备选题中一次性随机抽取
道备选题中一次性随机抽取 道题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中
道题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中 道题的便可通过.已知
道题的便可通过.已知 道题能正确完成,
道题能正确完成, ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响. 的分布列如右:其中
的分布列如右:其中 成等差数列,若
成等差数列,若 ,则
,则 的值是 .
的值是 .





