题目内容
设面积为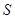 的平面四边形的第
的平面四边形的第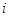 条边的边长记为
条边的边长记为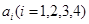 ,
,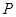 是该四边形内任意一点,
是该四边形内任意一点,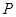 点到第
点到第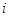 条边的距离记为
条边的距离记为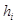 ,若
,若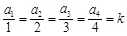 , 则
, 则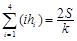 类比上述结论,体积为
类比上述结论,体积为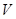 的三棱锥的第
的三棱锥的第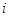 个面的面积记为
个面的面积记为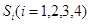 ,
,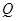 是该三棱锥内的任意一点,
是该三棱锥内的任意一点,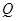 点到第
点到第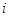 个面的距离记为
个面的距离记为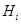 ,则相应的正确命题是:若
,则相应的正确命题是:若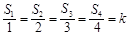 ,则 .
,则 .
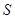 的平面四边形的第
的平面四边形的第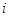 条边的边长记为
条边的边长记为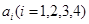 ,
,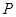 是该四边形内任意一点,
是该四边形内任意一点,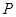 点到第
点到第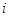 条边的距离记为
条边的距离记为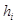 ,若
,若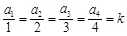 , 则
, 则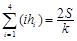 类比上述结论,体积为
类比上述结论,体积为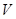 的三棱锥的第
的三棱锥的第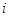 个面的面积记为
个面的面积记为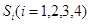 ,
,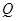 是该三棱锥内的任意一点,
是该三棱锥内的任意一点,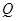 点到第
点到第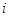 个面的距离记为
个面的距离记为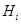 ,则相应的正确命题是:若
,则相应的正确命题是:若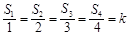 ,则 .
,则 . 
解:根据三棱锥的体积公式 V="1" /3 Sh
得:1 /3 S1H1+1 /3 S2H2+1 /3 S3H3+1 /3 S4H4=V,
即S1H1+2S2H2+3S3H3+4S4H4=3V,
∴H1+2H2+3H3+4H4="3V" /K ,
即 .
.
故答案为:3V /k .
得:1 /3 S1H1+1 /3 S2H2+1 /3 S3H3+1 /3 S4H4=V,
即S1H1+2S2H2+3S3H3+4S4H4=3V,
∴H1+2H2+3H3+4H4="3V" /K ,
即
 .
.故答案为:3V /k .

练习册系列答案
相关题目
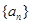 满足
满足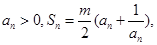 其中
其中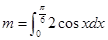 .
.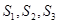 ,猜想
,猜想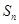 ;(II)请用数学归纳法证明之.
;(II)请用数学归纳法证明之. 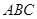 中,
中,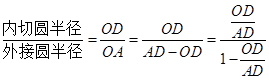 ,
,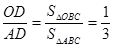 ,所以
,所以 。应用类比推理,在正四面体
。应用类比推理,在正四面体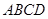 (每个面都是正三角形的四面体)中,
(每个面都是正三角形的四面体)中,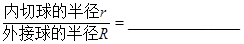 。
。 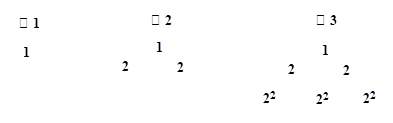
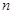 (
(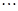 )有
)有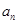 ,例如
,例如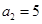 ,
,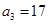 ,
,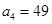 .则
.则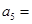 .
.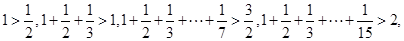 ……,
……,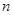 个式子应是____________________________________________.
个式子应是____________________________________________.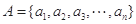 ,记和
,记和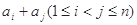 中所有不同值的个数为
中所有不同值的个数为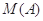 .如当
.如当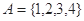 时,由
时,由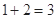 ,
,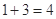 ,
,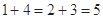 ,
,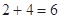 ,
,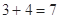 ,得
,得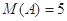 .对于集合
.对于集合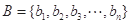 ,若实数
,若实数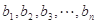 成等差数列,则
成等差数列,则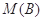 =
= 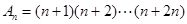 ,则
,则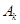 与
与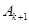 的关系为 ( )
的关系为 ( )