题目内容
已知向量 ,求满足|
,求满足| |<1的实数x的取值范围.
|<1的实数x的取值范围.
【答案】分析:利用两个向量数量积公式求出 ,即可得到|
,即可得到| |,解绝对值不等式|
|,解绝对值不等式| |=|x2+x-1|<1,求出其解集.
|=|x2+x-1|<1,求出其解集.
解答:解:∵ ,
,
∴ =-1+
=-1+ =x2+x-1.
=x2+x-1.
所以| |=|x2+x-1|<1,
|=|x2+x-1|<1,
所以-1<x2+x-1<1.
解得-2<x<0,或 0<x<1,故满足| |<1的实数x的取值范围为{x|-2<x<0,或 0<x<1 }.
|<1的实数x的取值范围为{x|-2<x<0,或 0<x<1 }.
点评:本题主要考查一元二次不等式的解法、绝对值不等式的解法,两个向量数量积公式的应用,属于中档题.
 ,即可得到|
,即可得到| |,解绝对值不等式|
|,解绝对值不等式| |=|x2+x-1|<1,求出其解集.
|=|x2+x-1|<1,求出其解集.解答:解:∵
 ,
,∴
 =-1+
=-1+ =x2+x-1.
=x2+x-1.所以|
 |=|x2+x-1|<1,
|=|x2+x-1|<1,所以-1<x2+x-1<1.
解得-2<x<0,或 0<x<1,故满足|
 |<1的实数x的取值范围为{x|-2<x<0,或 0<x<1 }.
|<1的实数x的取值范围为{x|-2<x<0,或 0<x<1 }.点评:本题主要考查一元二次不等式的解法、绝对值不等式的解法,两个向量数量积公式的应用,属于中档题.

练习册系列答案
相关题目
 ,求满足
,求满足 的实数
的实数 的取值范围
的取值范围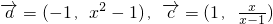 ,求满足|
,求满足| |<1的实数x的取值范围.
|<1的实数x的取值范围.