题目内容
已知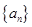 为等差数列,且
为等差数列,且 .
.
(Ⅰ)求数列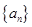 的通项公式及其前
的通项公式及其前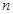 项和
项和 ;
;
(Ⅱ)若数列 满足
满足 求数列
求数列 的通项公式.
的通项公式.
(Ⅰ)  ,
, ;(Ⅱ)
;(Ⅱ)  .
.
解析试题分析:(Ⅰ)先设出等差数列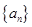 的首项和公差,然后代入式子:
的首项和公差,然后代入式子: ,列方程组求出首项和公差,再根据等差数列的通项公式:
,列方程组求出首项和公差,再根据等差数列的通项公式: 以及前
以及前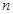 项和公式:
项和公式: 求解;(Ⅱ)由式子
求解;(Ⅱ)由式子 ,取
,取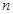 为
为 得到:
得到: ,两式相减得,
,两式相减得, ,结合(Ⅰ)的结果化简整理得,
,结合(Ⅰ)的结果化简整理得, ①,然后求出
①,然后求出 的值,代入①验证,要是不符合那么就把通项写成分段函数的形式,要是符合就合二为一写成一个式子.
的值,代入①验证,要是不符合那么就把通项写成分段函数的形式,要是符合就合二为一写成一个式子.
试题解析:(Ⅰ)设等差数列的首项和公差分别为 ,
,
则 ,解得
,解得 . 2分
. 2分
∴ , 4分
, 4分 6分
6分
(Ⅱ) ①,
①, ②, 7分
②, 7分
① ②得 , 8分
, 8分
∴ , 10分
, 10分 , 11分
, 11分
∴ . 12分
. 12分
考点:1.等差数列的通项公式;2.等差数列的前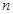 项和;3.数列的递推公式
项和;3.数列的递推公式

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 满足
满足 ,且对任意非负整数
,且对任意非负整数 均有:
均有: .
. ;
; 是等差数列,并求
是等差数列,并求 的通项;
的通项; ,求证:
,求证: .
. ,公差
,公差 不为零,
不为零,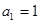 ,且
,且 成等比数列;
成等比数列; 满足
满足 ,求数列
,求数列 项和
项和 .
.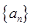 是首项为
是首项为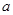 ,公差为
,公差为 的等差数列
的等差数列 ,
, 是其前
是其前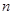 项和.
项和. ,
, ,求数列
,求数列 ,
, ,且
,且 、
、 、
、 成等比数列,证明:
成等比数列,证明: .
.
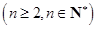 的两个数列
的两个数列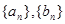 满足
满足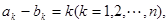 且集合
且集合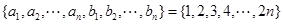 ,则称数列
,则称数列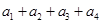 和
和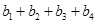 的值,并写出一对“
的值,并写出一对“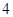 项
项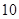 项相关数列”
项相关数列” 的前
的前 项和为
项和为 ,且
,且 是
是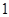 的等差中项,等差数列
的等差中项,等差数列 满足
满足 ,
, .
. ,数列
,数列 的前
的前 ,证明:
,证明: .
.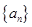 满足:
满足: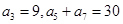 ,
,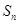 .
.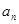 及
及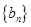 的第n项为
的第n项为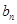 ,若
,若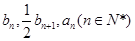 成等差数列,且
成等差数列,且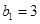 ,设数列
,设数列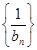 的前
的前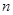 项和
项和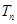 .求数列
.求数列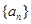 、
、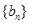 满足
满足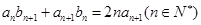 .
.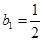 时,求数列
时,求数列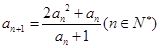 ,
,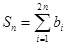 ,求证:
,求证: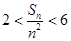 .
.