Question

（2012•石景山区一模）我区高三期末统一测试中某校的数学成绩分组统计如表：

分组	频数	频率
（0，30]	3	0.03
（30，60]	3	0.03
（60，90]	37	0.37
（90，120]	m	n
（120，150]	15	0.15
合计	M	N

（Ⅰ）求出表中m、n、M、N的值，并根据表中所给数据在下面给出的
坐标系中画出频率分布直方图；
（Ⅱ）若我区参加本次考试的学生有600人，试估计这次测试中我区成绩在90分以上的人数；
（Ⅲ）若该校教师拟从分数不超过60的学生中选取2人进行个案分析，求被选中2人分数不超过30分的概率．

Answer 1

分析：（I）根据频率公式，结合表中第一组数据的频率算出总数M．再用减法可得第五组的频数m，由此可算出第五组的频率n的值，而N是各组的频率之和，显然为1．
（II）90分以上的人有两组，分别是第五、六两组，算出它们的频率之和为0.57，由此不难估算出这次测试中我区成绩在90分以上的人数．
（III）根据题意，列出从不超过60分的6人中，任意抽取2人的结果有15种，而分数不超过30分的结果有3种，再结合等可能事件的概率公式，可得要求的概率．

解答：解：（I）由频率分布表，得总数M=

3

0.03

=100，…（1分）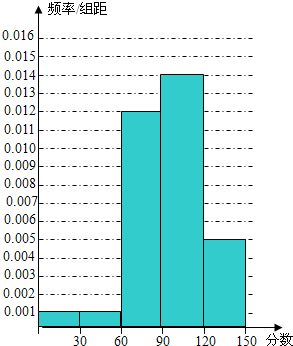
所以m=100-（3+3+37+15）=42，…（2分）
得第四组的频率n=

42

100

=0.42，
N=0.03+0.03+0.37+0.42+0.15=1．  …（3分）
所求的频率分布直方图如右图所示…（5分）
（Ⅱ）由题意，90分以上的人分别在第五组和第六组，
它们的频率之和为0.42+0.15=0.57，
∴全区90分以上学生估计为0.57×600=342人．…（7分）
（III）设考试成绩在（0，30]内的3人分别为A、B、C；
考试成绩在（30，60]内的3人分别为a、b、c，
从不超过60分的6人中，任意抽取2人的结果有：
（A，B），（A，C），（A，a），（A，b），（A，c），
（B，C），（B，a），（B，b），（B，c），（C，a），
（C，b），（C，c），（a，b），（a，c），（b，c）
共有15个．…（10分）
设抽取的2人的分数均不大于30分的事件为事件D．
则事件D含有3个结果：（A，B），（A，C），（B，C）   …（11分）
∴被选中2人分数不超过30分的概率为P(D)=

3

15

=

1

5

．                              …（13分）

点评：本题给出频率分布表，要我们计算其中的频率和频数，并算出被选中2人分数不超过30分的概率．着重考查了频率分布直方图的认识和等可能性事件的概率等知识，属于基础题．