题目内容
(2009•聊城二模)已知x,y满足
且目标函数z=3x+y的最小值是5,则z的最大值是( )
|
分析:由目标函数z=3x+y的最小值为5,我们可以画出满足条件的可行域,结合目标函数的解析式形式,分析取得最优解的点的坐标,然后根据分析列出一个含参数c的方程组,消参后即可得到c的取值,然后求出此目标函数的最大值即可.
解答: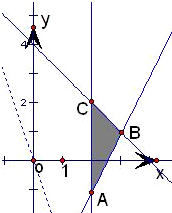 解:画出x,y满足的可行域如下图:
解:画出x,y满足的可行域如下图:
可得直线x=2与直线-2x+y+c=0的交点A,使目标函数z=3x+y取得最小值5,
故由
,
解得 x=2,y=4-c,
代入3x+y=5得
6+4-c=5,⇒c=5,
由
⇒B(3,1)
当过点B(3,1)时,目标函数z=3x+y取得最大值,最大值为10.
故选A.
 解:画出x,y满足的可行域如下图:
解:画出x,y满足的可行域如下图:可得直线x=2与直线-2x+y+c=0的交点A,使目标函数z=3x+y取得最小值5,
故由
|
解得 x=2,y=4-c,
代入3x+y=5得
6+4-c=5,⇒c=5,
由
|
当过点B(3,1)时,目标函数z=3x+y取得最大值,最大值为10.
故选A.
点评:如果约束条件中含有参数,我们可以先画出不含参数的几个不等式对应的平面区域,分析取得最优解是哪两条直线的交点,然后得到一个含有参数的方程(组),代入另一条直线方程,消去x,y后,即可求出参数的值.

练习册系列答案
相关题目