题目内容
（2009•聊城二模）已知关于x的不等式|3x-1|＜a有唯一的整数解，则方程（1-|2x-1|）ax=1实数根的个数为（ ）
分析：先根据关于x的不等式|3x-1|＜a有唯一的整数解求出a的取值范围，然后将方程（1-|2x-1|）ax=1实数根的个数可转化成y=1-|2x-1|与y=a-x图象的交点，结合图形可得结论．
解答：解：当a≤0时，不等式|3x-1|＜a没有整数解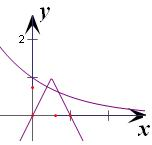
当a＞0时，解得
＜x＜
在
附近的整数有0与1，当包含1时有两个整数，不合题意
∴不等式的整数解为0，则
＜0，
＜1
解得1＜a＜2
方程（1-|2x-1|）ax=1实数根的个数可转化成y=1-|2x-1|与y=a-x图象的交点
分别画出函数y=1-|2x-1|与y=a-x的图象
根据可知有两个交点，则方程（1-|2x-1|）ax=1实数根有2个
故选C．
当a＞0时，解得
| 1-a |
| 3 |
| 1+a |
| 3 |
在
| 1 |
| 3 |
∴不等式的整数解为0，则
| 1-a |
| 3 |
| 1+a |
| 3 |
解得1＜a＜2
方程（1-|2x-1|）ax=1实数根的个数可转化成y=1-|2x-1|与y=a-x图象的交点
分别画出函数y=1-|2x-1|与y=a-x的图象
根据可知有两个交点，则方程（1-|2x-1|）ax=1实数根有2个
故选C．
点评：本题主要考查了根的存在性及根的个数判断，解决此类问题常常转化成两函数图象的交点问题，同时考查了数形结合的思想，属于中档题．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目