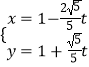题目内容
【题目】抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形,阿基米德三角形有一些有趣的性质,如:若抛物线的弦过焦点,则过弦的端点的两条切线的交点在其准线上.设抛物线![]()
![]() >
>![]() ,弦AB过焦点,△ABQ为其阿基米德三角形,则△ABQ的面积的最小值为
,弦AB过焦点,△ABQ为其阿基米德三角形,则△ABQ的面积的最小值为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】分析:设![]() ,设直线
,设直线![]() 方程与抛物线方程联立可求得焦点弦的性质
方程与抛物线方程联立可求得焦点弦的性质![]() ,设切线方程分别与抛物线方程联立可求得两切线的斜率之间的的关系,得两切线相互垂直,从而知
,设切线方程分别与抛物线方程联立可求得两切线的斜率之间的的关系,得两切线相互垂直,从而知![]() ,因此有
,因此有![]() ,当
,当![]() 最小时,三角形面积最小.
最小时,三角形面积最小.
详解:如图所示,设![]() ,则
,则![]() ,
,

设直线![]() ,联立
,联立 ,
,
化为![]() ,
,
∴![]() ,
,![]() .
.
设过![]() 点的切线为
点的切线为![]() ,
,
由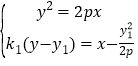 得
得![]() ,
,
∵直线为切线,
∴![]() ,化简得
,化简得![]() ,
,
同理设过![]() 点的切线斜率为
点的切线斜率为![]() ,可得
,可得![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,即两切线垂直,
,即两切线垂直,![]() 是直角三角形.
是直角三角形.
∴![]() ,当且仅当
,当且仅当![]() 为通径时等号成立.
为通径时等号成立.
![]() ,
,
∴当![]() 最小时,
最小时,![]() 最小.即
最小.即![]() 的最小值为
的最小值为![]() .
.
故选B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】为了巩固全国文明城市创建成果,今年吉安市开展了拆除违章搭建铁皮棚专项整治行为.为了了解市民对此项工作的“支持”与“反对”态度,随机从存在违章搭建的户主中抽取了男性、女性共![]() 名进行调查,调查结果如下:
名进行调查,调查结果如下:
支持 | 反对 | 合计 | |
男性 |
|
|
|
女性 |
|
|
|
合计 |
|
|
|
(1)根据以上数据,判断是否有![]() 的把握认为对此项工作的“支持”与“反对”态度与“性别”有关;
的把握认为对此项工作的“支持”与“反对”态度与“性别”有关;
(2)现从参与调查的女户主中按分层抽样的方法抽取![]() 人进行调查,分别求出所抽取的
人进行调查,分别求出所抽取的![]() 人中持“支持”和“反对”态度的人数;
人中持“支持”和“反对”态度的人数;
(3)现从(2)中所抽取的![]() 人中,再随机抽取
人中,再随机抽取![]() 人赠送小品,求恰好抽到
人赠送小品,求恰好抽到![]() 人持“支持”态度的概率?
人持“支持”态度的概率?
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|