题目内容
在△ABC中,S为△ABC的面积,且S=c2-(a-b)2
(1)求tanC
(2)当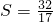 时,求ab的值.
时,求ab的值.
解:在△ABC中,由正弦定理得: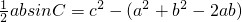 ,
,
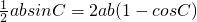 ,
,
∴sinC=4(1-cosC),
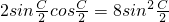 ,
,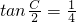 ,
,
 ,
,
∵C∈(0,π),
∴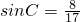 ,
,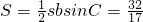 ,
,
∴ab=8.
分析:(1)将正弦定理中三角形的面积公式与余弦定理结合可得到sinC=4(1-cosC),利用三角函数的升幂公式可求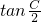 ,从而可求tanC;
,从而可求tanC;
(2)由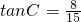 ,sinC=4(1-cosC),可求sinC的值,利用
,sinC=4(1-cosC),可求sinC的值,利用 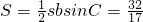 即可求ab的值.
即可求ab的值.
点评:本题考查正弦定理,三角函数的降幂公式与半角公式的灵活运用是难点,属于中档题.
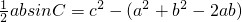 ,
,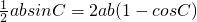 ,
,∴sinC=4(1-cosC),
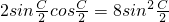 ,
,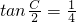 ,
, ,
,∵C∈(0,π),
∴
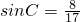 ,
,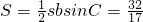 ,
,∴ab=8.
分析:(1)将正弦定理中三角形的面积公式与余弦定理结合可得到sinC=4(1-cosC),利用三角函数的升幂公式可求
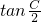 ,从而可求tanC;
,从而可求tanC;(2)由
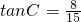 ,sinC=4(1-cosC),可求sinC的值,利用
,sinC=4(1-cosC),可求sinC的值,利用 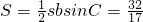 即可求ab的值.
即可求ab的值.点评:本题考查正弦定理,三角函数的降幂公式与半角公式的灵活运用是难点,属于中档题.

练习册系列答案
相关题目
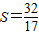 时,求ab的值.
时,求ab的值.