题目内容
在△ABC中,S为△ABC的面积,且S=c2-(a-b)2
(1)求tanC
(2)当S=
时,求ab的值.
(1)求tanC
(2)当S=
| 32 |
| 17 |
在△ABC中,由正弦定理得:
absinC=c2-(a2+b2-2ab),
absinC=2ab(1-cosC),
∴sinC=4(1-cosC),
2sin
cos
=8sin2
,tan
=
,
tanC=
=
,
∵C∈(0,π),
∴sinC=
,S=
sbsinC=
,
∴ab=8.
| 1 |
| 2 |
| 1 |
| 2 |
∴sinC=4(1-cosC),
2sin
| C |
| 2 |
| C |
| 2 |
| C |
| 2 |
| C |
| 2 |
| 1 |
| 4 |
tanC=
2tan
| ||
1-tan2
|
| 8 |
| 15 |
∵C∈(0,π),
∴sinC=
| 8 |
| 17 |
| 1 |
| 2 |
| 32 |
| 17 |
∴ab=8.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
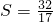 时,求ab的值.
时,求ab的值.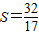 时,求ab的值.
时,求ab的值.