题目内容
设奇函数
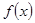 在
在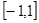 上是增函数,且
上是增函数,且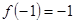 ,当
,当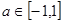 时,
时, 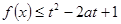 对所有的
对所有的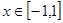 恒成立,则
恒成立,则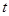 的取值范围是( )
的取值范围是( )A. 或 或 或 或 | B. 或 或 |
C. 或 或 或 或 | D. |
A
本题考查函数的单调性的应用,函数的最值,不等式与函数的关系,函数思想及转化思想.
奇函数 在
在 上是增函数,且,
上是增函数,且, 所以函数
所以函数 在
在 上的最大值为
上的最大值为 当
当 时,
时, 对所有的
对所有的 恒成立,等价于
恒成立,等价于 当
当 时恒成立;整理得
时恒成立;整理得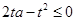 当
当 时恒成立;设
时恒成立;设 ;则问题等价于
;则问题等价于 ,解得
,解得 所以
所以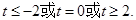 故选A
故选A
奇函数
 在
在 上是增函数,且,
上是增函数,且, 所以函数
所以函数 在
在 上的最大值为
上的最大值为 当
当 时,
时, 对所有的
对所有的 恒成立,等价于
恒成立,等价于 当
当 时恒成立;整理得
时恒成立;整理得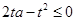 当
当 时恒成立;设
时恒成立;设 ;则问题等价于
;则问题等价于 ,解得
,解得 所以
所以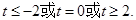 故选A
故选A
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. 时,求函数
时,求函数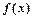 的定义域;
的定义域; ,试求
,试求 的取值范围
的取值范围
 在
在 上是增函数,在
上是增函数,在 上是减函数,则 ( )
上是减函数,则 ( ) <0
<0 的两个实根一个小于
的两个实根一个小于 ,另一个大于
,另一个大于 的取值范围是
的取值范围是 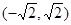


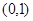
 的图像经过坐
的图像经过坐 标原
标原 ,设函数
,设函数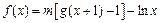 ,其中m为常数且
,其中m为常数且 。
。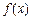 的单调性并说明理由。
的单调性并说明理由。
 和“伪二次函数”
和“伪二次函数”
 (
( 、
、 、
、
 ),
), ,无论
,无论 在定义域内不可能总为增函数;
在定义域内不可能总为增函数; ,线段
,线段 中点的横坐标为
中点的横坐标为 ,记直线
,记直线 ,
,  i)求证:
i)求证: ;
; ,是否有(i)同样的性质?证明你的结论.
,是否有(i)同样的性质?证明你的结论. 

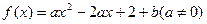 ,在区间
,在区间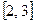 上有最大值5,最小
上有最大值5,最小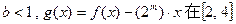 上单调,求
上单调,求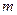 的取值范围。
的取值范围。