题目内容
18.设函数f(n)=(1+$\frac{1}{n}$)n-n,其中n为正整数.(1)求f(1)、f(2)、f(3)的值;
(2)猜想满足不等式f(n)<0的正整数n的范围,并用数学归纳法证明你的猜想.
分析 (1)由f(n)=(1+$\frac{1}{n}$)n-n,可求得f(1),f(2),f(3)的值;
(2)猜想:n≥3,f(n)=(1+$\frac{1}{n}$)n-n<0,再利用数学归纳法证明即可:①当n=3时,f(3)=-$\frac{17}{27}$<0成立;②假设当n=k(n≥3,n∈N+)时猜想正确,即f(k)=$(1+\frac{1}{k})^{k}$-k<0,去证明当n=k+1(n≥3,n∈N+)时,f(k+1)=(1+$\frac{1}{k+1}$)k+1-(k+1)<0也成立即可.
解答 解:(1)∵f(n)=(1+$\frac{1}{n}$)n-n,
∴f(1)=1,f(2)=$(1+\frac{1}{2})^{2}$-2=$\frac{1}{4}$,f(3)=$(1+\frac{1}{3})^{3}$-3=-$\frac{17}{27}$,…(3分)
(2)猜想:n≥3,f(n)=(1+$\frac{1}{n}$)n-n<0,…(4分)
证明:①当n=3时,f(3)=-$\frac{17}{27}$<0成立,…(5分)
②假设当n=k(n≥3,n∈N+)时猜想正确,即f(k)=$(1+\frac{1}{k})^{k}$-k<0,
∴$(1+\frac{1}{k})^{k}$<k,
则当n=k+1时,
由于f(k+1)=(1+$\frac{1}{k+1}$)k+1=(1+$\frac{1}{k+1}$)k(1+$\frac{1}{k+1}$)=$(1+\frac{1}{k})^{k}$(1+$\frac{1}{k+1}$)
<k(1+$\frac{1}{k+1}$)<k+1,…(8分)
∴(1+$\frac{1}{k+1}$)k+1<k+1,即f(k+1)=(1+$\frac{1}{k+1}$)k+1-(k+1)<0成立,
由①②可知,对n≥3,f(n)=(n)=(1+$\frac{1}{n}$)n-n<0成立.…(10分)
点评 本题考查数学归纳法,考查运算、推理及论证能力,属于中档题.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案
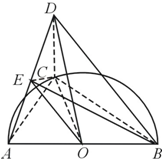 如图,已知点C是圆心为O半径为1的半圆弧上从点A数起的第一个三等分点,AB是直径,CD=1,CD⊥平面ABC,点E是AD的中点.
如图,已知点C是圆心为O半径为1的半圆弧上从点A数起的第一个三等分点,AB是直径,CD=1,CD⊥平面ABC,点E是AD的中点.