题目内容
【题目】已知函数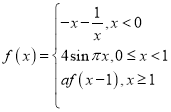
，若函数
的所有零点之和为
，则
的取值范围为______.
【答案】
【解析】
由题意结合函数的解析式和函数图象确定实数
的取值范围即可．
解：原问题转化为函数
与函数
交点的横坐标之和为
，
绘制函数在区间
上的图象如图所示，
当
时，
.
当
时，
绘制函数在区间上的图象如图所示，
所以当时，函数与函数交点的横坐标为：
，
由函数
与在上的交点有两个，
根据函数的对称性有，这两个交点关于直线
对称。
所以函数与在上的两个交点的横坐标之和为1.
所以函数与在
上的三个交点的横坐标之和为0.
因此原问题转化为函数与函数在
上的交点的横坐标之和为
当
，则函数与函数在区间
上各有两个交点.
显然这些交点的横坐标之和大于3.所以
当
，若函数与函数在区间
上有两个交点，则根据对称性，这两个交点横坐标之和刚好为3.
则函数与函数在区间
上没有交点.
所以结合函数的函数图象可知：
.
求解不等式组可得实数的取值范围为：.
当
时，则函数与函数在区间上没有交点，不满足条件.
当
时，则函数与函数在区间上要么没有交点，要么交点的横坐标之和等于
或大于3，皆不满足条件.
故答案为：.
练习册系列答案
教学练新同步练习系列答案
相关题目
