Question

已知函数f(x)＝－x3＋ax2－4(a∈R)．

(1)若函数y＝f(x)的图象在点P(1，f(1))处的切线的倾斜角为，求f(x)在[－1,1]上的最小值；

(2)若存在x0∈(0，＋∞)，使f(x0)＞0，求a的取值范围．

 

Answer 1

(1) 最小值为f(0)＝－4 (2) (3，＋∞)

【解析】(1)f′(x)＝－3x2＋2ax.

根据题意得，f′(1)＝tan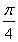＝1，∴－3＋2a＝1，即a＝2.

∴f(x)＝－x3＋2x2－4，则f′(x)＝－3x2＋4x.

令f′(x)＝0，得x1＝0，x2＝.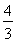

x	－1	(－1,0)	0	(0,1)	1
f′(x)		－	0	＋
f(x)	－1	?	－4	?	－3

∴当x∈[－1,1]时，f(x)的最小值为f(0)＝－4.

(2)∵f′(x)＝－3x.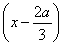

①若a≤0，则当x>0时，f′(x)<0，∴f(x)在(0，＋∞)上单调递减．

又f(0)＝－4，则当x＞0时，f(x)＜－4.

∴当a≤0时，不存在x0＞0，使f(x0)＞0.

②若a＞0，则当0＜x＜时，f′(x)＞0；

当x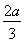＞时，f′(x)＜0.

从而f(x)在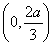上单调递增，在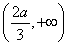上单调递减．

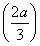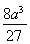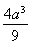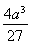∴当x∈(0，＋∞)时，f(x)max＝f＝－＋－4＝－4.

根据题意得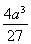，－4＞0，即a3＞27.∴a＞3.

综上可知，a的取值范围是(3，＋∞)．