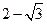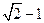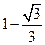题目内容
已知多面体 中,
中,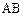
 平面
平面 ,
, ∥
∥ ,
,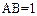 ,
, ,
, 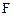 、
、 分别为
分别为 、
、 的中点.
的中点.
(Ⅰ)求证:
 面
面 ;
;
(Ⅱ)求三棱锥 的体积.
的体积.
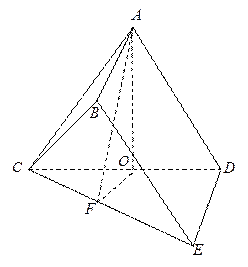
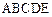 中,
中,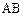
 平面
平面 ,
, ∥
∥ ,
,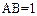 ,
, ,
, 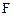 、
、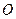 分别为
分别为 、
、 的中点.
的中点.(Ⅰ)求证:

 面
面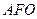 ;
;(Ⅱ)求三棱锥
 的体积.
的体积.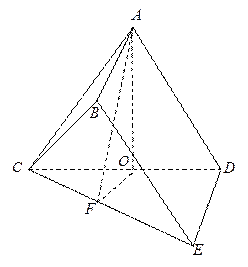
(II)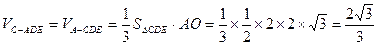

解:(I)∵

 平面
平面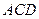
 ∥
∥
∴

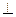 平面
平面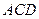 ∴
∴ 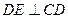
∵
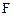 、
、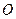 分别为
分别为 、
、 的中点.
的中点.∴
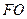 ∥
∥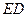 ∴
∴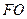
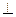

∵
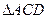 是等边三角形 ∴
是等边三角形 ∴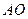
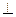

∴

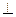 面
面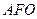 …………………6分
…………………6分(II) ∵
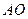
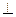
 ,
, 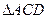 是等边三角形
是等边三角形∴
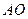
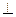 面
面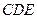 ∴
∴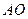 是三棱锥
是三棱锥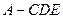 的高
的高∴
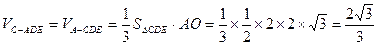 …………12分
…………12分
练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
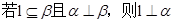
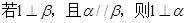
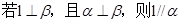
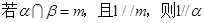
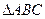 中∠ACB=90°,AS=BC=1,AC=2,SA⊥面ABC,AD⊥SC于D,
中∠ACB=90°,AS=BC=1,AC=2,SA⊥面ABC,AD⊥SC于D,
 的球内有一内接正三棱锥,它的底面三个顶点恰好都在同一个大圆
的球内有一内接正三棱锥,它的底面三个顶点恰好都在同一个大圆 B.
B. C.
C. D.
D.
 为底面的棱柱被平面
为底面的棱柱被平面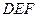 所截而得,已
所截而得,已 知
知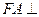 平面
平面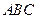 ,
,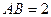 ,
,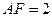 ,
,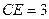 ,
,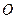 为
为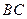 的中点,
的中点,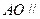 面
面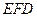 .
.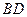 的长;
的长;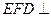 面
面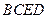 ;
;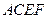 相交所成锐角二面角的余弦值.
相交所成锐角二面角的余弦值.
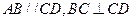 ,侧面SAB为等边三角形,
,侧面SAB为等边三角形,
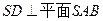 ;
; 求AB与平面SBC所成的角的大小。
求AB与平面SBC所成的角的大小。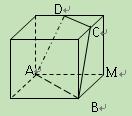
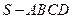 的底面是正方形,且
的底面是正方形,且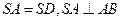 ,
,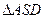 的面积为
的面积为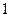 ,则能够放入这个棱锥的最大球的半径为
,则能够放入这个棱锥的最大球的半径为