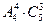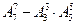题目内容
设(5x-)n的展开式的各项系数之和为M, 二项式系数之和为N,若M-N=240, 则展开式中x3的系数为( )
| A.-150 | B.150 |
| C.-500 | D.500 |
B
分析:利用赋值法及二项式系数和公式求出M、N列出方程求得n,利用二项展开式的通项公式求出第r+1项,令x的指数为3得系数.
解:(5x-)n中,令x=1得展开式的各项系数之和M=4n
根据二项式系数和公式得二项式系数之和N=2n
∵M-N=240
∴4n-2n=240解得n=4
∴(5x-)n=(5x-)4的展开式的通项为Tr+1=
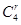 (5X)4-r(-)r=(-1)r54-r
(5X)4-r(-)r=(-1)r54-r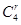 x4-
x4-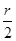
令4-
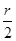 =3得r=2
=3得r=2故展开式中x3的系数为52C42=150
故选项为B

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 =21,那么n="___________" .
=21,那么n="___________" . 的展开式中第4项为常数项,则
的展开式中第4项为常数项,则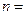 ________
________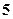 个班到
个班到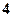 个社区进
个社区进 行社会实践,每个班去一个社区,每个社区至少安排一个班,不同的安排方法共有 种(用数
行社会实践,每个班去一个社区,每个社区至少安排一个班,不同的安排方法共有 种(用数 字作答)
字作答)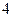 名男同学和
名男同学和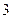 名女同学排成一排照相,且女同学互不相邻,不同排法的种数为
名女同学排成一排照相,且女同学互不相邻,不同排法的种数为