题目内容
【题目】已知命题p:k2﹣8k﹣20≤0,命题q:方程 ![]() =1表示焦点在x轴上的双曲线. (Ⅰ)命题q为真命题,求实数k的取值范围;
=1表示焦点在x轴上的双曲线. (Ⅰ)命题q为真命题,求实数k的取值范围;
(Ⅱ)若命题“p∨q”为真,命题“p∧q”为假,求实数k的取值范围.
【答案】解:(Ⅰ)当命题q为真时,由已知得 ![]() ,解得1<k<4 ∴当命题q为真命题时,实数k的取值范围是1<k<4
,解得1<k<4 ∴当命题q为真命题时,实数k的取值范围是1<k<4
(Ⅱ)当命题p为真时,由k2﹣8k﹣20≤0解得﹣2≤k≤10
由题意得命题p、q中有一真命题、有一假命题
当命题p为真、命题q为假时,则  ,
,
解得﹣2≤k≤1或4≤k≤10
当命题p为假、命题q为真时,则 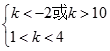 ,k无解.
,k无解.
∴实数k的取值范围是﹣2≤k≤1或4≤k≤10.
【解析】(Ⅰ)命题q为真命题,由已知得 ![]() ,可求实数k的取值范围;(Ⅱ)根据题意得命题p、q有且仅有一个为真命题,分别讨论“p真q假”与“p假q真”即可得出实数a的取值范围.
,可求实数k的取值范围;(Ⅱ)根据题意得命题p、q有且仅有一个为真命题,分别讨论“p真q假”与“p假q真”即可得出实数a的取值范围.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目