题目内容
16.平面直角坐标系xOy中,P是不在x轴上一个动点,满足条件:过P可作抛物线y2=4x的两条切线,两切点连线lP与PO垂直,设直线lP与PO,x轴的交点分别为Q,R.(1)证明:R是一个定点;
(2)求$\frac{|PQ|}{|QR|}$的最小值.
分析 (1)求出直线lP的方程为ny=2(m+x),利用两切点连线lP与PO垂直,$\frac{2}{n}×\frac{n}{m}$=-1,即可得证;
(2)直线PO的方程为y=$\frac{n}{m}$x=-$\frac{n}{2}$x,代入直线lP的方程,求得Q的坐标,进而得到|PQ|,|QR|,运用基本不等式即可得到最小值.
解答 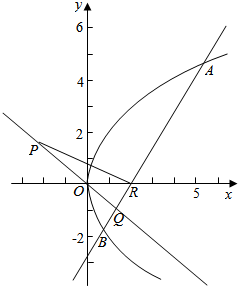 (1)证明:设以A(x1,y1)为切点的切线方程为y-y1=k(x-x1),
(1)证明:设以A(x1,y1)为切点的切线方程为y-y1=k(x-x1),
联立抛物线方程,可得ky2-4y+4y1-4kx1=0,
由△=4(2-ky1)2=0,
得k=$\frac{2}{{y}_{1}}$,所以切线PA:y1y=2(x+x1)
同理以B(x2,y2)为切点的切线方程为y2y=2(x+x2),
设P(m,n),则ny1=2(m+x1),ny2=2(m+x2),
∴直线lP的方程为ny=2(m+x),
∵两切点连线lP与PO垂直,
∴$\frac{2}{n}×\frac{n}{m}$=-1,
∴m=-2,
∴直线lP的方程为ny=2(x-2),
∴R(2,0)为定点;
(2)解:直线PO的方程为y=$\frac{n}{m}$x=-$\frac{n}{2}$x,代入直线lP的方程,求得Q($\frac{8}{{n}^{2}+4}$,$\frac{-4n}{{n}^{2}+4}$),
∴|PQ|=$\sqrt{(\frac{8}{{n}^{2}+4}+2)^{2}+(\frac{4n}{{n}^{2}+4}+n)^{2}}$=$\frac{({n}^{2}+8)\sqrt{{n}^{2}+4}}{{n}^{2}+4}$,
|QR|=$\sqrt{(\frac{8}{{n}^{2}+4}-2)^{2}+(\frac{4n}{{n}^{2}+4})^{2}}$=$\frac{2n\sqrt{{n}^{2}+4}}{{n}^{2}+4}$,
如图,由对称性,不妨取n>0,则$\frac{|PQ|}{|QR|}$=$\frac{1}{2}$(n+$\frac{8}{n}$)≥2$\sqrt{2}$,∴求$\frac{|PQ|}{|QR|}$的最小值为2$\sqrt{2}$.
点评 本题考查抛物线的方程和性质,主要考查抛物线的方程的运用,联立直线方程,运用判别式为0,同时考查直线垂直的条件,考查运算求解能力,属于中档题.

| A. | {1} | B. | {0,1,2} | C. | {0,1} | D. | {1,2} |