题目内容
17．定义在R上的函数f′（x）=kx+b，其中常数k＞0，则函数f（x）（ ）| A． | 在（-∞，+∞）上递增 | B． | 在[-$\frac{b}{k}$，+∞）上递增 | C． | 在（-∞，-$\frac{b}{k}$）上递增 | D． | 在（-∞，+∞）上递减 |
分析 由导数的运算性质，可设f（x）=$\frac{1}{2}$kx2+bx+c（k＞0，c为常数），由二次函数的单调性，可得单调区间．
解答 解：定义在R上的函数f′（x）=kx+b，
可设f（x）=$\frac{1}{2}$kx2+bx+c（k＞0，c为常数），
对称轴为x=-$\frac{b}{k}$，
则f（x）在（-∞，-$\frac{b}{k}$）上递减，
在（-$\frac{b}{k}$，+∞）递增．
故选：B．
点评 本题考查导数的运算性质，考查二次函数的单调性的判断，属于基础题．
练习册系列答案
初中学业考试导与练系列答案
相关题目
8．若a+b=m${\;}^{\frac{1}{3}}$，ab=$\frac{1}{6}$m${\;}^{\frac{2}{3}}$（a＞b），则a3+b3的值为（ ）
| A． | 0 | B． | $\frac{m}{2}$ | C． | -$\frac{m}{2}$ | D． | $\frac{3}{2}$m |
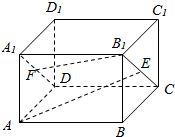如图，在长方体ABCD-A1B1C1D1中，E是矩形BCC1B1的中点，F是矩形ADD1A1的中心，连接AE，B1F，判断AE与B1F是否为异面直线．