题目内容
已知△ABC的三内角的大小成等差数列,tgAtgC= 求角A,B,C的大小,又已知顶点C的对边c上的高等于
求角A,B,C的大小,又已知顶点C的对边c上的高等于 ,求三角形各边a,b,c的长.(提示:必要时可验证
,求三角形各边a,b,c的长.(提示:必要时可验证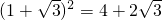 )
)
解:A+B+C=180°又2B=A+C.∴B=60°,A+C=120°
∵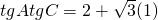
而tgA+tgC=(1-tgAtgC)tg(A+C)=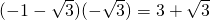 .(2)
.(2)
由(1)(2)可知tgA,tgC是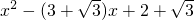 =0的两根.解这方程得:
=0的两根.解这方程得:
x1=1,x2=2+ 设A<C,则得tgA=1,tgC=2+
设A<C,则得tgA=1,tgC=2+ .
.
∴A=45°,C=120°-45°=75°又知c上的高等于4 ,
,
∴a=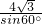 =8;b=
=8;b=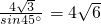 ;
;
c=AD+DB=bcos45°+acos60°=4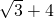 .
.
分析:△ABC的三内角的大小成等差数列,求出B=60°,A+C=120°,利用两角和的正切,求出tgA+tgC,然后求出tgA,tgC,求出A,C的值,利用任意角的三角函数求出a,b,c.
点评:本题考查同角三角函数基本关系的运用,等差数列的性质,三角形中的几何计算,考查计算能力,是中档题.
∵
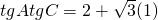
而tgA+tgC=(1-tgAtgC)tg(A+C)=
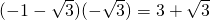 .(2)
.(2)由(1)(2)可知tgA,tgC是
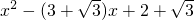 =0的两根.解这方程得:
=0的两根.解这方程得:x1=1,x2=2+
 设A<C,则得tgA=1,tgC=2+
设A<C,则得tgA=1,tgC=2+ .
.∴A=45°,C=120°-45°=75°又知c上的高等于4
 ,
,∴a=
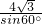 =8;b=
=8;b=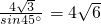 ;
;c=AD+DB=bcos45°+acos60°=4
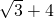 .
.分析:△ABC的三内角的大小成等差数列,求出B=60°,A+C=120°,利用两角和的正切,求出tgA+tgC,然后求出tgA,tgC,求出A,C的值,利用任意角的三角函数求出a,b,c.
点评:本题考查同角三角函数基本关系的运用,等差数列的性质,三角形中的几何计算,考查计算能力,是中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
已知△ABC的三内角A,B,C成等差数列,则 tan(A+C)=( )
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|