题目内容
设函数f(x)=bcosx+csinx的图象经过两点(0,1)和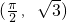 ,对一切x∈[0,π],|f(x)+a|≤3恒成立,则实数a的取值范围________.
,对一切x∈[0,π],|f(x)+a|≤3恒成立,则实数a的取值范围________.
[-2,1]
分析:依题意可求得b=1,c= ,从而可根据x∈[0,π],|f(x)+a|≤3恒成立,利用正弦函数的性质解决.
,从而可根据x∈[0,π],|f(x)+a|≤3恒成立,利用正弦函数的性质解决.
解答:依题意得:f(0)=bcos0+csin0=b=1,
f( )=bcos
)=bcos +csin
+csin =c=
=c= ,
,
∴f(x)=cosx+ sinx=2sin(x+
sinx=2sin(x+ ).
).
又x∈[0,π],
∴ ≤x+
≤x+ ≤
≤ ,
,
∴- ≤sin(x+
≤sin(x+ )≤1,
)≤1,
∴-1≤2sin(x+ )≤2,即-1≤f(x)≤2,
)≤2,即-1≤f(x)≤2,
∴-2≤-f(x)≤1;
∵|f(x)+a|≤3恒成立,
∴-3≤f(x)+a≤3,
∴-3-f(x)≤a≤3-f(x).
∴a≥[-3-f(x)]max=-2且a≤[3-f(x)]min=1,
∴-2≤a≤1.
∴实数a的取值范围为[-2,1].
故答案为:[-2,1].
点评:本题考查绝对值不等式的解法,考查两角和与差的正弦函数与正弦函数的单调性,考查综合分析与应用能力,属于难题.
分析:依题意可求得b=1,c=
 ,从而可根据x∈[0,π],|f(x)+a|≤3恒成立,利用正弦函数的性质解决.
,从而可根据x∈[0,π],|f(x)+a|≤3恒成立,利用正弦函数的性质解决.解答:依题意得:f(0)=bcos0+csin0=b=1,
f(
 )=bcos
)=bcos +csin
+csin =c=
=c= ,
,∴f(x)=cosx+
 sinx=2sin(x+
sinx=2sin(x+ ).
).又x∈[0,π],
∴
 ≤x+
≤x+ ≤
≤ ,
,∴-
 ≤sin(x+
≤sin(x+ )≤1,
)≤1,∴-1≤2sin(x+
 )≤2,即-1≤f(x)≤2,
)≤2,即-1≤f(x)≤2,∴-2≤-f(x)≤1;
∵|f(x)+a|≤3恒成立,
∴-3≤f(x)+a≤3,
∴-3-f(x)≤a≤3-f(x).
∴a≥[-3-f(x)]max=-2且a≤[3-f(x)]min=1,
∴-2≤a≤1.
∴实数a的取值范围为[-2,1].
故答案为:[-2,1].
点评:本题考查绝对值不等式的解法,考查两角和与差的正弦函数与正弦函数的单调性,考查综合分析与应用能力,属于难题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 设函数f(x)=
设函数f(x)= 选考题
选考题