题目内容
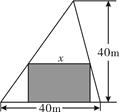
已知矩形ABCD,AB=8,BC=6,按以下两种方法将其折叠为两部分,设两部分的面积为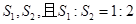 ,折痕为线段EF,问用哪一种方法折叠,折痕EF最长?并求EF长度的最大值.
,折痕为线段EF,问用哪一种方法折叠,折痕EF最长?并求EF长度的最大值.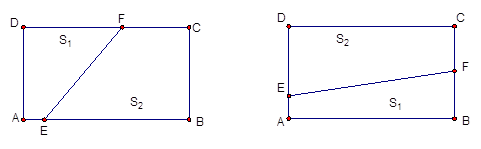
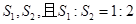 ,折痕为线段EF,问用哪一种方法折叠,折痕EF最长?并求EF长度的最大值.
,折痕为线段EF,问用哪一种方法折叠,折痕EF最长?并求EF长度的最大值.

试题分析:解:图1:设AE=x,DF=y,则
 3分
3分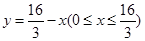 4分
4分 7分
7分图2:设AE="x," BF=y,则
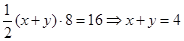 10分
10分 11分
11分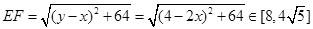 14分
14分综上:
 16分
16分点评:主要是考查了不等式来求解最值的运用,属于中档题。

练习册系列答案
相关题目
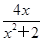 的最大值为________________________.
的最大值为________________________. ,则
,则 的最小值是 .
的最小值是 . ,若不等式
,若不等式 恒成立,则实数
恒成立,则实数 的最大值是______.
的最大值是______.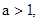 则
则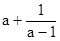 的最小值是 ( )
的最小值是 ( )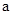
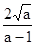
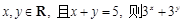 的最小值是( )
的最小值是( )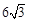
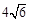
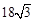
 ,
, ,
, .则下列不等式:①
.则下列不等式:① ; ②
; ② ; ③
; ③ ; ④
; ④ .其中成立的是 .(写出所有正确命题的序号)
.其中成立的是 .(写出所有正确命题的序号)  ,则函数
,则函数 的最大值是__________
的最大值是__________