题目内容
如图所示,在以AB为直径的半圆周上,有异于A,B的六个点C1,C2,…,C6,直径AB上有异于A,B的四个点D1,D2,D3,D4.则:
(1)以这12个点(包括A,B)中的4个点为顶点,可作出多少个四边形?
(2)以这10个点(不包括A,B)中的3个点为顶点,可作出多少个三角形?其中含点C1的有多少个?
(1)360 (2)36
解析解:(1)构成四边形,需要四个点,且无三点共线,可以分成三类:
①四个点从C1,C2,…,C6中取出,有C64个四边形;
②三个点从C1,C2,…,C6中取出,另一个点从D1,D2,D3,D4,A,B中取出,有C63C61个四边形;
③二个点从C1,C2,…,C6中取出,另外二个点从D1,D2,D3,D4,A,B中取出,有C62C62个四边形.
故满足条件的四边形共有
N=C64+C63C61+C62C62=360(个).
(2)类似于(1)可分三种情况讨论得三角形个数为
C63+C61C42+C62C41=116(个).
其中含点C1的有C52+C51C41+C42=36(个).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
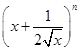 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列. 的展开式中,第6项
的展开式中,第6项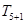 为常数项.
为常数项.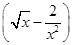 8的展开式中,
8的展开式中,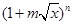 (
( 是正实数)的展开式的二项式系数之和为256,展开式中含
是正实数)的展开式的二项式系数之和为256,展开式中含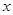 项的系数为112.
项的系数为112.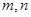 的值;
的值;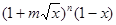 的展开式中含
的展开式中含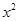 项的系数.
项的系数.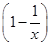 3的展开式中的常数项为a,求
3的展开式中的常数项为a,求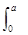 (3x2-1)dx.
(3x2-1)dx.