题目内容
已知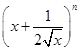 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.
(1)求n的值;
(2)求展开式中系数最大的项.
(1)8;(2)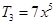 ,
,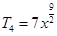 .
.
解析试题分析:(1)由二项展开式通项求出前三项的系数,再利用已知前三项系数成等差数列和等差中项的概念,列出关于n的方程,解出n;(2)设第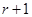 项系数最大,利用二项展开式的通项求出第
项系数最大,利用二项展开式的通项求出第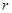 项系数、第
项系数、第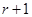 项系数、第
项系数、第 项的系数,再利用第
项的系数,再利用第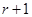 项系数最大即其不小于前一项的系数也不小于后一项的系数,列出关于r的方程,解出r的值.
项系数最大即其不小于前一项的系数也不小于后一项的系数,列出关于r的方程,解出r的值.
试题解析:(1)由题设,得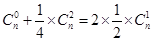 , 即
, 即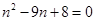 ,
,
解得n=8或n=1(舍去). 6分
(2)设第r+1的系数最大,则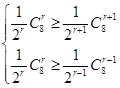 即
即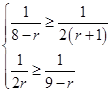 10分
10分
解得r=2或r=3. 12分
所以系数最大的项为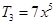 ,
,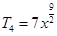 . 14分
. 14分
考点:等差中项;二项定理;二项式系数最大值

练习册系列答案
相关题目
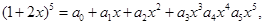 则a3= 。
则a3= 。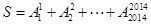 ,记
,记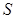 的个位上的数字为
的个位上的数字为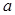 ,十位上的数字
,十位上的数字 ,求
,求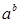 的值;
的值; (结果不必用具体数字表示).
(结果不必用具体数字表示).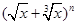 (其中n<15)的展开式中:
(其中n<15)的展开式中:
 展开式中
展开式中 的系数是 。
的系数是 。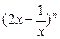 的展开式中二项式系数之和为128,则展开式中
的展开式中二项式系数之和为128,则展开式中 的系数是_______
的系数是_______