题目内容
定义在(-1,1)上的函数f(x)满足:①对任意x,y∈(-1,1),都有f(x)+f(y)=f(
);②f(x)在(-1,1)上是单调递增函数,f(
)=1.
(1)求f(0)的值;
(2)证明:f(x)为奇函数;
(3)解不等式f(2x-1)<1.
| x+y |
| 1+xy |
| 1 |
| 2 |
(1)求f(0)的值;
(2)证明:f(x)为奇函数;
(3)解不等式f(2x-1)<1.
分析:(1)通过赋值法,x=y=0,求出f(0)=0;
(2)说明函数f(x)的奇偶性,通过令y=-x,推出对于任意的x∈R,恒有f(-x)=-f(x),f(x)为奇函数.
(3)f(2x-1)<1即f(2x-1)<f(
),根据函数的单调性,即可求满足f(2x-1)<1的实数x的集合.
(2)说明函数f(x)的奇偶性,通过令y=-x,推出对于任意的x∈R,恒有f(-x)=-f(x),f(x)为奇函数.
(3)f(2x-1)<1即f(2x-1)<f(
| 1 |
| 2 |
解答:解:(1)取x=y=0,则f(0)+f(0)=f(0),
∴f(0)=0
(2)令y=-x∈(-1,1),则f(x)+f(-x)=f(
)=f(0)=0,
∴f(-x)=-f(x)
则f(x)在(-1,1)上为奇函数.
(3)不等式可化为
⇒
⇒0<x<
∴解集为(0,
)
∴f(0)=0
(2)令y=-x∈(-1,1),则f(x)+f(-x)=f(
| x-x |
| 1-x2 |
∴f(-x)=-f(x)
则f(x)在(-1,1)上为奇函数.
(3)不等式可化为
|
|
| 3 |
| 4 |
∴解集为(0,
| 3 |
| 4 |
点评:本题是综合题,考查赋值法求函数值的应用,函数奇偶性的判断与证明,函数图象的应用,不等式的解法.运算能力,理解能力要求比较高.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目
 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.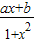 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.