题目内容
【题目】已知函数,f(x)=![]() -mx2-m+ln(1-m),(m<1).
-mx2-m+ln(1-m),(m<1).
(Ⅰ)当m=![]() 时,求f(x)的极值;
时,求f(x)的极值;
(Ⅱ)证明:函数f(x)有且只有一个零点.
【答案】(Ⅰ)函数极大值为![]() ,极小值为
,极小值为 ![]() ;(Ⅱ)见解析
;(Ⅱ)见解析
【解析】
(Ⅰ)利用导数,通过![]() 的符号,判断出函数的单调性,找到极值点,可得结果.
的符号,判断出函数的单调性,找到极值点,可得结果.
(Ⅱ)计算![]() ,采用分类讨论的方法,
,采用分类讨论的方法,![]() ,
,![]() 以及
以及![]() ,判断函数的单调性,可得结果.
,判断函数的单调性,可得结果.
(Ⅰ)![]()
![]() ,则
,则![]() 在
在![]() 递增,
递增,
在![]() 递减,在
递减,在![]() 上递增,
上递增,
所以函数极大值为![]() ,
,
极小值为![]() .
.
(Ⅱ)![]()
①当![]() 时,
时,![]() ,
,
![]() 只有一个零点0,符合题意;
只有一个零点0,符合题意;
②当![]() 时,
时,![]() 在
在![]() 单调递增,
单调递增,
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
![]() ,
,
令![]() ,
,![]() ,
,
显然![]() 单调递减,有
单调递减,有![]() ,即
,即![]() ,
,
则![]() 只有一个零点,符合题意;
只有一个零点,符合题意;
③当![]() 时,
时,![]() 在
在![]() 单调递增,
单调递增,
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
![]() ,
,![]() ,由②构造的函数知,
,由②构造的函数知,
![]() ,
,
则![]() 只有一个零点,符合题意.
只有一个零点,符合题意.
综上所述,![]() 时,函数
时,函数![]() 有且只有一个零点.
有且只有一个零点.

 阅读快车系列答案
阅读快车系列答案【题目】每年10月中上旬是小麦的最佳种植时间,但小麦的发芽会受到土壤、气候等多方面因素的影响.某科技小组为了解昼夜温差的大小与小麦发芽的多少之间的关系,在不同的温差下统计了100颗小麦种子的发芽数,得到了如下数据:
温差 | 8 | 10 | 11 | 12 | 13 |
发芽数 | 79 | 81 | 85 | 86 | 90 |
(1)请根据统计的最后三组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若由(1)中的线性回归方程得到的估计值与前两组数据的实际值误差均不超过两颗,则认为线性回归方程是可靠的,试判断(1)中得到的线性回归方程是否可靠;
(3)若100颗小麦种子的发芽率为![]() 颗,则记为
颗,则记为![]() 的发芽率,当发芽率为
的发芽率,当发芽率为![]() 时,平均每亩地的收益为
时,平均每亩地的收益为![]() 元,某农场有土地10万亩,小麦种植期间昼夜温差大约为
元,某农场有土地10万亩,小麦种植期间昼夜温差大约为![]() ,根据(1)中得到的线性回归方程估计该农场种植小麦所获得的收益.
,根据(1)中得到的线性回归方程估计该农场种植小麦所获得的收益.
附:在线性回归方程![]() 中,
中,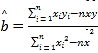 .
.
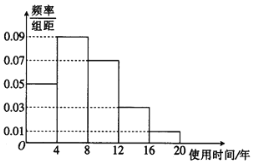
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:![]() )得频率分布直方图如下:
)得频率分布直方图如下:


(1)设两种养殖方法的箱产量相互独立,记![]() 表示事件:“旧养殖法的箱产量低于
表示事件:“旧养殖法的箱产量低于![]() ,新养殖法的箱产量不低于
,新养殖法的箱产量不低于![]() ”,估计
”,估计![]() 的概率;
的概率;
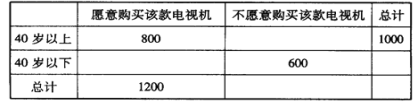
(2)填写下面![]() 列联表,并根据联表判断是否有
列联表,并根据联表判断是否有![]() 的把握认为箱产量与养殖方法有关:
的把握认为箱产量与养殖方法有关:
箱产量 | 箱产量 | |
旧养殖法 | ||
新养殖法 |
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(3)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01)
【题目】随着电子商务的发展, 人们的购物习惯正在改变, 基本上所有的需求都可以通过网络购物解决. 小韩是位网购达人, 每次购买商品成功后都会对电商的商品和服务进行评价. 现对其近年的200次成功交易进行评价统计, 统计结果如下表所示.
对服务好评 | 对服务不满意 | 合计 | |
对商品好评 | 80 | 40 | 120 |
对商品不满意 | 70 | 10 | 80 |
合计 | 150 | 50 | 200 |
(1) 是否有![]() 的把握认为商品好评与服务好评有关? 请说明理由;
的把握认为商品好评与服务好评有关? 请说明理由;
(2) 若针对商品的好评率, 采用分层抽样的方式从这200次交易中取出5次交易, 并从中选择两次交易进行观察, 求只有一次好评的概率.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(![]() ,其中
,其中![]() )
)