题目内容
(2012•顺河区一模)偶函数f(x)满足f(x-2)=f(x+2),且在x∈[0,2]时,f(x)=2cos
x,则关于x的方程f(x)=(
)x,在x∈[-2,6]上解的个数是( )
| π |
| 4 |
| 1 |
| 2 |
分析:根据题意,函数f(x)是周期为4的是偶函数,在[0,2]上的表达式为f(x)=2cos
x,由此不难作出f(x)在[-2,6]上的图象,再在同一坐标系内作出函数y=(
)x的图象,观察两个图象的交点个数,即得本题方程实数根的个数.
| π |
| 4 |
| 1 |
| 2 |
解答:解:∵当x∈[0,2]时,0≤
x≤
,f(x)=2cos
x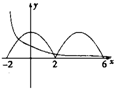
∴函数f(x)在x=0时,函数值有最大值f(0)=2cos0=2,
在x=2时,函数值有最小值f(2)=2cos
=0.
由此作出函数f(x)在x∈[0,2]时的图象,呈减函数趋势如图
∵函数f(x)是偶函数,
∴f(x)在[-2,0]上的图象与[0,2]上的图象关于y轴对称,如图所示
∵函数f(x)满足f(x-2)=f(x+2),∴函数f(x)是周期T=4的周期函数.
因此,将f(x)在[-2,2]上的图象向右平移一个周期,得f(x)在[2,6]上的图象
∴函数f(x)在[-2,6]上的图象如右图所示,是位于x轴上方的两段余弦型曲线弧
在同一坐标系内作出函数y=(
)x的图象,可得它经过点(0,1),呈减函数趋势如图
因为两个图象有4个交点,得关于x的方程f(x)=(
)x的实数根也有4个
故选D
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |

∴函数f(x)在x=0时,函数值有最大值f(0)=2cos0=2,
在x=2时,函数值有最小值f(2)=2cos
| π |
| 2 |
由此作出函数f(x)在x∈[0,2]时的图象,呈减函数趋势如图
∵函数f(x)是偶函数,
∴f(x)在[-2,0]上的图象与[0,2]上的图象关于y轴对称,如图所示
∵函数f(x)满足f(x-2)=f(x+2),∴函数f(x)是周期T=4的周期函数.
因此,将f(x)在[-2,2]上的图象向右平移一个周期,得f(x)在[2,6]上的图象
∴函数f(x)在[-2,6]上的图象如右图所示,是位于x轴上方的两段余弦型曲线弧
在同一坐标系内作出函数y=(
| 1 |
| 2 |
因为两个图象有4个交点,得关于x的方程f(x)=(
| 1 |
| 2 |
故选D
点评:本题以一个关于x的方程根的个数讨论为载体,考查了函数的单调性与奇偶性、基本初等函数图象作法和函数的周期等知识点,属于中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
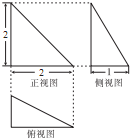 (2012•顺河区一模)三棱椎A-BCD的三视图为如图所示的三个直角三角形,则三棱锥A-BCD的表面积为( )
(2012•顺河区一模)三棱椎A-BCD的三视图为如图所示的三个直角三角形,则三棱锥A-BCD的表面积为( )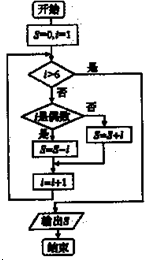 (2012•顺河区一模)执行如图所给的程序框图,则运行后输出的结果是( )
(2012•顺河区一模)执行如图所给的程序框图,则运行后输出的结果是( )