题目内容
(2012•顺河区一模)已知函数f(x)=ln
-ax2+x(a>0).
(1)若f(x)是单调函数,求a的取值范围;
(2)若f(x)有两个极值点x1,x2,证明:f(x1)+f(x2)>3-2ln2.
| 1 | x |
(1)若f(x)是单调函数,求a的取值范围;
(2)若f(x)有两个极值点x1,x2,证明:f(x1)+f(x2)>3-2ln2.
分析:(1)先由f(x),求出f′(x)=-
-2ax+1=-
.再利用导数判断函数的单调性,由f(x)是单调函数,能求出a的取值范围.
(2)由(1)知,当且仅当a∈(0,
)时,f(x)有极小值点x1和极大值点x2,且x1+x2=
,x1x2=
.求得f(x1)+f(x2)=-ln(x1x2)+
(x1+x2)+1=ln(2a)+
+1.令g(a)=ln(2a)+
+1,a∈(0,
],由此能够证明f(x1)+f(x2)>3-2ln2.
| 1 |
| x |
| 2ax2-x+1 |
| x |
(2)由(1)知,当且仅当a∈(0,
| 1 |
| 8 |
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 2 |
| 1 |
| 4a |
| 1 |
| 4a |
| 1 |
| 8 |
解答:解:(Ⅰ)f(x)=-lnx-ax2+x,
f′(x)=-
-2ax+1=-
.…(2分)
令△=1-8a.
当a≥
时,△≤0,f′(x)≤0,f(x)在(0,+∞)单调递减.…(4分)
当0<a<
时,△>0,方程2ax2-x+1=0有两个不相等的正根x1,x2,
不妨设x1<x2,
则当x∈(0,x1)∪(x2,+∞)时,f′(x)<0,
当x∈(x1,x2)时,f′(x)>0,
这时f(x)不是单调函数.
综上,a的取值范围是[
,+∞).…(6分)
(Ⅱ)由(Ⅰ)知,当且仅当a∈(0,
)时,f(x)有极小值点x1和极大值点x2,
且x1+x2=
,x1x2=
.
f(x1)+f(x2)=-lnx1-ax12+x1-lnx2-ax22+x2
=-(lnx1+lnx2)-
(x1-1)-
(x2-1)+(x1+x2)
=-ln(x1x2)+
(x1+x2)+1=ln(2a)+
+1.…(9分)
令g(a)=ln(2a)+
+1,a∈(0,
],
则当a∈(0,
)时,g′(a)=
-
=
<0,g(a)在(0,
)单调递减,
所以g(a)>g(
)=3-2ln2,即f(x1)+f(x2)>3-2ln2.…(12分)
f′(x)=-
| 1 |
| x |
| 2ax2-x+1 |
| x |
令△=1-8a.
当a≥
| 1 |
| 8 |
当0<a<
| 1 |
| 8 |
不妨设x1<x2,
则当x∈(0,x1)∪(x2,+∞)时,f′(x)<0,
当x∈(x1,x2)时,f′(x)>0,
这时f(x)不是单调函数.
综上,a的取值范围是[
| 1 |
| 8 |
(Ⅱ)由(Ⅰ)知,当且仅当a∈(0,
| 1 |
| 8 |
且x1+x2=
| 1 |
| 2a |
| 1 |
| 2a |
f(x1)+f(x2)=-lnx1-ax12+x1-lnx2-ax22+x2
=-(lnx1+lnx2)-
| 1 |
| 2 |
| 1 |
| 2 |
=-ln(x1x2)+
| 1 |
| 2 |
| 1 |
| 4a |
令g(a)=ln(2a)+
| 1 |
| 4a |
| 1 |
| 8 |
则当a∈(0,
| 1 |
| 8 |
| 1 |
| a |
| 1 |
| 4a2 |
| 4a-1 |
| 4a2 |
| 1 |
| 8 |
所以g(a)>g(
| 1 |
| 8 |
点评:本题考查实数取值范围的求法,考查不等式的证明,综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意导数性质的合理运用.

练习册系列答案
相关题目
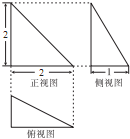 (2012•顺河区一模)三棱椎A-BCD的三视图为如图所示的三个直角三角形,则三棱锥A-BCD的表面积为( )
(2012•顺河区一模)三棱椎A-BCD的三视图为如图所示的三个直角三角形,则三棱锥A-BCD的表面积为( )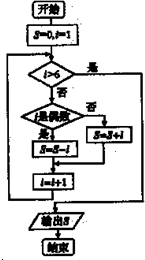 (2012•顺河区一模)执行如图所给的程序框图,则运行后输出的结果是( )
(2012•顺河区一模)执行如图所给的程序框图,则运行后输出的结果是( )