题目内容
(本题满分13分)
已知抛物线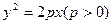 的焦点为F,直线
的焦点为F,直线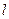 过定点
过定点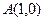 且与抛物线交于P,Q两点。
且与抛物线交于P,Q两点。
(1)若以弦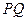 为直径的圆恒过原点
为直径的圆恒过原点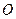 ,求p的值;
,求p的值;
(2)在(1)的条件下,若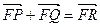 ,求动点R的轨迹方程。
,求动点R的轨迹方程。
已知抛物线
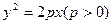 的焦点为F,直线
的焦点为F,直线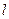 过定点
过定点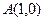 且与抛物线交于P,Q两点。
且与抛物线交于P,Q两点。(1)若以弦
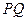 为直径的圆恒过原点
为直径的圆恒过原点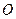 ,求p的值;
,求p的值;(2)在(1)的条件下,若
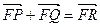 ,求动点R的轨迹方程。
,求动点R的轨迹方程。(1)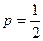
(2)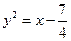
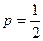
(2)
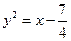
解:<1>①若直线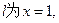 将
将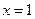 带入
带入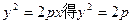 ,
,
以弦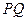 为直径的圆恒过原点O,有
为直径的圆恒过原点O,有
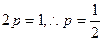 ………………2分
………………2分
②若直线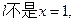 设直线方程为:
设直线方程为: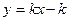 ,将
,将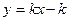 代入
代入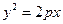 得
得 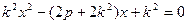
设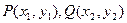 ,则由韦达定理得:
,则由韦达定理得: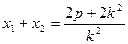
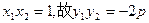
以弦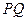 为直径的圆恒过原点O,
为直径的圆恒过原点O,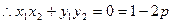 ,
,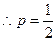
又此时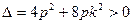 ,综合①②得
,综合①②得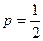 …………6分
…………6分
<2>设动点R的坐标为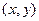
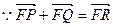
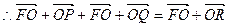
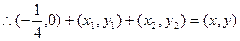
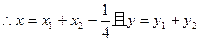
①当直线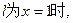
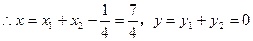 …9分
…9分
②当直线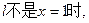
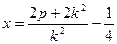
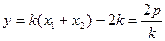 …11分
…11分
即得: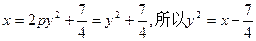
又因为点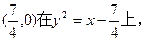
所以由①②得R点的轨迹方程为: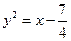 ………………13分
………………13分
点评:此题也可设直线方程为: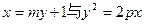 联立求解。
联立求解。
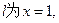 将
将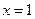 带入
带入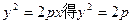 ,
,以弦
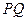 为直径的圆恒过原点O,有
为直径的圆恒过原点O,有
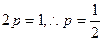 ………………2分
………………2分②若直线
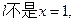 设直线方程为:
设直线方程为: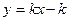 ,将
,将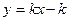 代入
代入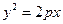 得
得 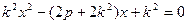
设
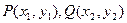 ,则由韦达定理得:
,则由韦达定理得: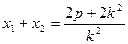
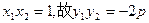
以弦
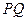 为直径的圆恒过原点O,
为直径的圆恒过原点O,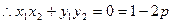 ,
,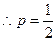
又此时
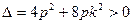 ,综合①②得
,综合①②得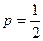 …………6分
…………6分<2>设动点R的坐标为
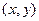
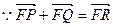
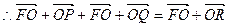
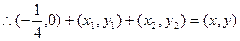
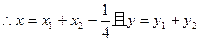
①当直线
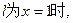
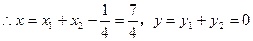 …9分
…9分②当直线
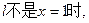
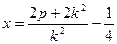
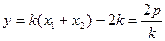 …11分
…11分即得:
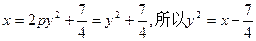
又因为点
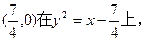
所以由①②得R点的轨迹方程为:
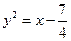 ………………13分
………………13分 点评:此题也可设直线方程为:
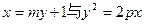 联立求解。
联立求解。
练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
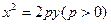 相交于B、C两点,当l的斜率是
相交于B、C两点,当l的斜率是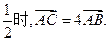
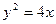 上的点
上的点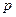 到抛物线的准线的距离为
到抛物线的准线的距离为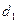 ,到直线
,到直线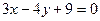 的距离为
的距离为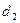 ,则
,则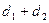 的最小值为 ( )
的最小值为 ( )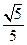
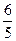
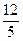
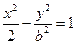 (a>0,b>0)的渐近线与抛物线
(a>0,b>0)的渐近线与抛物线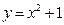 相切,则b等于( )
相切,则b等于( )



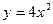 的准线方程为 ( )
的准线方程为 ( )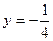
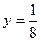
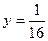
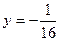
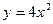 的准线方程为
的准线方程为 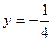
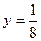

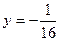
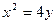 的焦点F作直线交抛物线于
的焦点F作直线交抛物线于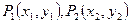 两点,若
两点,若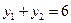 ,则
,则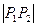 的值为 ( )
的值为 ( ) 上一点,
上一点, ,
, 是其焦点,若
是其焦点,若 ,则
,则 的范围是
的范围是



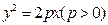 的顶点
的顶点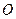 的两弦
的两弦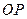 ,
,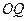 互相垂直,求以
互相垂直,求以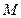 的轨迹方程。
的轨迹方程。