Question

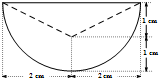（2012•深圳二模）某零件的正（主）视图与侧（左）视图均是如图所示的图形（实线组成半径为2cm的半圆，虚线是等腰三角形的两腰），俯视图是一个半径为2cm的圆（包括圆心），则该零件的体积是（　　）

• A．

  4

  3

  πcm³
• B．

  8

  3

  πcm³
• C．4πcm³
• D．

  20

  3

  πcm³

Answer 1

分析：由三视图可知此几何体为半球与圆锥构成的简单组合体，以及球的半径，圆锥的底面半径与高，
进而可求出各简单几何体的体积，继而得到组合体的体积．

解答：解：由三视图知，此几何体为半球与圆锥构成的简单组合体，
且半球的半径为2cm，圆锥的底面半径是2cm，高是1cm．
所以该几何体的体积V=

1

2

×

4

3

πr3-

1

3

πr2×h=

12π

3

=4π (cm3)．
故答案选 C．

点评：本题考查了几何体的三视图，以及球和圆锥的体积．常见的几何体的表面积、体积公式一定要记住．