题目内容
已知△ABC的角A、B、C所对的边分别是a、b、c,设向量
=(a,b),
=(sinB,sinA),
=(b-2,a-2).
(1)若
∥
,求证:△ABC为等腰三角形;
(2)若
⊥
,边长c=2,角C=
,求△ABC的面积.
| m |
| n |
| p |
(1)若
| m |
| n |
(2)若
| m |
| p |
| π |
| 3 |
证明:(1)∵m∥n
∴asinA=bsinB
即a•
=b•
.其中R为△ABC外接圆半径.
∴a=b
∴△ABC为等腰三角形.
(2)由题意,m•p=0
∴a(b-2)+b(a-2)=0
∴a+b=ab
由余弦定理4=a2+b2-2ab•cos
∴4=a2+b2-ab=(a+b)2-3ab
∴ab2-3ab-4=0
∴ab=4或ab=-1(舍去)
∴S△ABC=
absinC
=
×4×sin
=
∴asinA=bsinB
即a•
| a |
| 2R |
| b |
| 2R |
∴a=b
∴△ABC为等腰三角形.
(2)由题意,m•p=0
∴a(b-2)+b(a-2)=0
∴a+b=ab
由余弦定理4=a2+b2-2ab•cos
| π |
| 3 |
∴4=a2+b2-ab=(a+b)2-3ab
∴ab2-3ab-4=0
∴ab=4或ab=-1(舍去)
∴S△ABC=
| 1 |
| 2 |
=
| 1 |
| 2 |
| π |
| 3 |
| 3 |

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
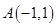 、
、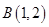 、
、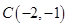 、
、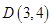 ,则向量
,则向量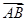 在
在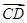 方向上的投影为 .
方向上的投影为 . 、
、 为两个不共线向量,则向量
为两个不共线向量,则向量 (
( )与向量
)与向量 共线的条件是
共线的条件是 =________.
=________. ________________
________________ 分
分 的比为
的比为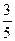 ,
, 、
、 ,则
,则 .
.